The z-Average of Cross-Linked Polymers

IF 1.8 4区工程技术 Q3 POLYMER SCIENCE

Macromolecular Theory and Simulations Pub Date : 2024-02-09 DOI:10.1002/mats.202300065

Rolf Bachmann

{"title":"The z-Average of Cross-Linked Polymers","authors":"Rolf Bachmann","doi":"10.1002/mats.202300065","DOIUrl":null,"url":null,"abstract":"Stockmayer's formula for the weight average of cross-linked primary chains is extended to the z-average degree of polymerization <math>\n <semantics>\n <mrow>\n <mi>D</mi>\n <msub>\n <mi>P</mi>\n <mi>z</mi>\n </msub>\n </mrow>\n <annotation>$DP_z$</annotation>\n </semantics></math>. This average is a function of the weight- and z-average degree of polymerization λw and λz of the primary chain distribution and the branching density α: <math>\n <semantics>\n <mrow>\n <mi>D</mi>\n <msub>\n <mi>P</mi>\n <mi>z</mi>\n </msub>\n <mo>=</mo>\n <mfrac>\n <mrow>\n <msub>\n <mi>λ</mi>\n <mi>z</mi>\n </msub>\n <msup>\n <mrow>\n <mo>(</mo>\n <mn>1</mn>\n <mo>+</mo>\n <mi>α</mi>\n <mo>)</mo>\n </mrow>\n <mn>3</mn>\n </msup>\n <mo>−</mo>\n <msubsup>\n <mi>λ</mi>\n <mi>w</mi>\n <mn>2</mn>\n </msubsup>\n <msup>\n <mi>α</mi>\n <mn>2</mn>\n </msup>\n <mrow>\n <mo>(</mo>\n <mn>3</mn>\n <mo>+</mo>\n <mi>α</mi>\n <mo>)</mo>\n </mrow>\n </mrow>\n <mrow>\n <msup>\n <mrow>\n <mo>(</mo>\n <mn>1</mn>\n <mo>−</mo>\n <mi>α</mi>\n <mrow>\n <mo>(</mo>\n <msub>\n <mi>λ</mi>\n <mi>w</mi>\n </msub>\n <mo>−</mo>\n <mn>1</mn>\n <mo>)</mo>\n </mrow>\n <mo>)</mo>\n </mrow>\n <mn>2</mn>\n </msup>\n <mrow>\n <mo>(</mo>\n <mn>1</mn>\n <mo>+</mo>\n <mi>α</mi>\n <mo>)</mo>\n </mrow>\n </mrow>\n </mfrac>\n </mrow>\n <annotation>$DP_z= \\frac{\\lambda _z(1+\\alpha)^3-\\lambda _w^2\\alpha ^2(3+\\alpha)}{(1-\\alpha (\\lambda _w-1))^2(1+\\alpha)}$</annotation>\n </semantics></math>. Higher averages of branched polymers from monomers of type <math>\n <semantics>\n <msub>\n <mi>A</mi>\n <mi>f</mi>\n </msub>\n <annotation>$A_f$</annotation>\n </semantics></math> and <math>\n <semantics>\n <mrow>\n <mi>B</mi>\n <msub>\n <mi>A</mi>\n <mrow>\n <mi>f</mi>\n <mo>−</mo>\n <mn>1</mn>\n </mrow>\n </msub>\n </mrow>\n <annotation>$BA_{f-1}$</annotation>\n </semantics></math> with functionalities f ⩾ 2 are discussed.","PeriodicalId":18157,"journal":{"name":"Macromolecular Theory and Simulations","volume":"33 3","pages":""},"PeriodicalIF":1.8000,"publicationDate":"2024-02-09","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Macromolecular Theory and Simulations","FirstCategoryId":"5","ListUrlMain":"https://onlinelibrary.wiley.com/doi/10.1002/mats.202300065","RegionNum":4,"RegionCategory":"工程技术","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"POLYMER SCIENCE","Score":null,"Total":0}

引用次数: 0

Abstract

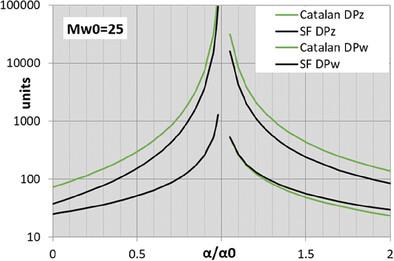
Stockmayer's formula for the weight average of cross-linked primary chains is extended to the z-average degree of polymerization $D P_{z}$ . This average is a function of the weight- and z-average degree of polymerization λ_w and λ_z of the primary chain distribution and the branching density α: $D P_{z} = \frac{λ_{z} {(1 + α)}^{3} - λ_{w}^{2} α^{2} (3 + α)}{{(1 - α (λ_{w} - 1))}^{2} (1 + α)}$ . Higher averages of branched polymers from monomers of type $A_{f}$ and $B A_{f - 1}$ with functionalities f ⩾ 2 are discussed.

Abstract Image

查看原文本刊更多论文

交联聚合物的 z 平均值

斯托克迈尔的交联主链重量平均值公式被扩展到 z 平均聚合度 DPz。该平均值是主链分布的重量平均聚合度 λw 和 z 平均聚合度 λz 以及支化密度 α 的函数：本文受版权保护。本文受版权保护。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Macromolecular Theory and Simulations 工程技术-高分子科学

CiteScore

3.00

自引率

14.30%

发文量

审稿时长

2 months

期刊介绍： Macromolecular Theory and Simulations is the only high-quality polymer science journal dedicated exclusively to theory and simulations, covering all aspects from macromolecular theory to advanced computer simulation techniques.