Regret analysis of an online majorized semi-proximal ADMM for online composite optimization

IF 1.8 3区数学 Q1 Mathematics

Journal of Global Optimization Pub Date : 2024-02-15 DOI:10.1007/s10898-024-01365-5

Zehao Xiao, Liwei Zhang

引用次数: 0

Abstract

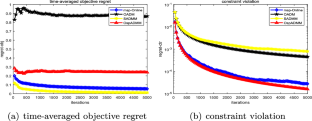
An online majorized semi-proximal alternating direction method of multiplier (Online-mspADMM) is proposed for a broad class of online linearly constrained composite optimization problems. A majorized technique is adopted to produce subproblems which can be easily solved. Under mild assumptions, we establish \(\mathcal {O}(\sqrt{N})\) objective regret and \(\mathcal {O}(\sqrt{N})\) constraint violation regret at round N. We apply the Online-mspADMM to solve different types of online regularized logistic regression problems. The numerical results on synthetic data sets verify the theoretical result about regrets.

Abstract Image

查看原文本刊更多论文

用于在线复合优化的在线主要半近似 ADMM 的遗憾分析

针对各类在线线性约束复合优化问题，提出了一种在线大化半近似交替方向乘法（Online-mspADMM）。该方法采用大化技术来生成易于求解的子问题。在温和的假设条件下，我们在第 N 轮建立了 \(\mathcal {O}(\sqrt{N})\) 目标遗憾和 \(\mathcal {O}(\sqrt{N})\) 约束违反遗憾。在合成数据集上的数值结果验证了关于遗憾的理论结果。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of Global Optimization 数学-应用数学

CiteScore

0.10

自引率

5.60%

发文量

137

审稿时长

6 months

期刊介绍： The Journal of Global Optimization publishes carefully refereed papers that encompass theoretical, computational, and applied aspects of global optimization. While the focus is on original research contributions dealing with the search for global optima of non-convex, multi-extremal problems, the journal’s scope covers optimization in the widest sense, including nonlinear, mixed integer, combinatorial, stochastic, robust, multi-objective optimization, computational geometry, and equilibrium problems. Relevant works on data-driven methods and optimization-based data mining are of special interest. In addition to papers covering theory and algorithms of global optimization, the journal publishes significant papers on numerical experiments, new testbeds, and applications in engineering, management, and the sciences. Applications of particular interest include healthcare, computational biochemistry, energy systems, telecommunications, and finance. Apart from full-length articles, the journal features short communications on both open and solved global optimization problems. It also offers reviews of relevant books and publishes special issues.