Examples of Nonpronormal Relatively Maximal Subgroups of Finite Simple Groups
IF 0.4
4区 数学
Q4 MATHEMATICS
Proceedings of the Steklov Institute of Mathematics
Pub Date : 2024-02-12
DOI:10.1134/s0081543823060135
引用次数: 0
Abstract
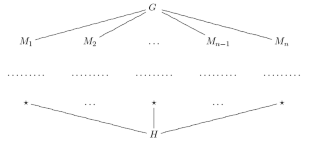
Using R. Wilson’s recent results, we prove the existence of triples \((\mathfrak{X},G,H)\) such that \(\mathfrak{X}\) is a complete (i.e., closed under taking subgroups, homomorphic images, and extensions) class of finite groups, \(G\) is a finite simple group, and \(H\) is its \(\mathfrak{X}\)-maximal subgroup nonpronormal in \(G\). This disproves a conjecture stated earlier by the second author and W. Guo.
有限简单群的非正则相对最大子群实例
利用 R. Wilson 的最新成果,我们证明了三元组 \((\mathfrak{X},G,H)\)的存在,使得 \(\mathfrak{X}\) 是一个完整的(即、(G)是一个有限简单群,而\(H)是它\(\mathfrak{X}\)-最大子群在\(G)中的非正则。)这推翻了第二作者和 W. Guo 早先提出的猜想。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Proceedings of the Steklov Institute of Mathematics
MATHEMATICS, APPLIED-MATHEMATICS
CiteScore
0.90
自引率
20.00%
发文量
24
审稿时长
4-8 weeks
期刊介绍:
Proceedings of the Steklov Institute of Mathematics is a cover-to-cover translation of the Trudy Matematicheskogo Instituta imeni V.A. Steklova of the Russian Academy of Sciences. Each issue ordinarily contains either one book-length article or a collection of articles pertaining to the same topic.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


