Fano 4-folds with $b_{2}>12$ are products of surfaces

Abstract

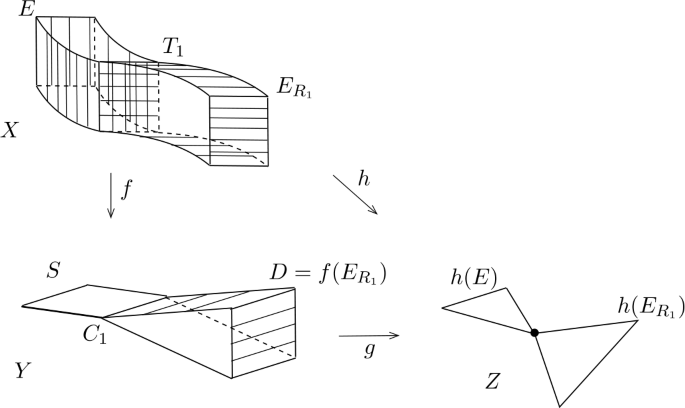
Let \(X\) be a smooth, complex Fano 4-fold, and \(\rho _{X}\) its Picard number. We show that if \(\rho _{X}>12\), then \(X\) is a product of del Pezzo surfaces. The proof relies on a careful study of divisorial elementary contractions \(f\colon X\to Y\) such that \(\dim f(\operatorname{Exc}(f))=2\), together with the author’s previous work on Fano 4-folds. In particular, given \(f\colon X\to Y\) as above, under suitable assumptions we show that \(S:=f(\operatorname{Exc}(f))\) is a smooth del Pezzo surface with \(-K_{S}=(-K_{Y})_{|S}\).