Susceptible-Exposed-Infectious Model Using Markov Chains
IF 1.4
4区 物理与天体物理
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
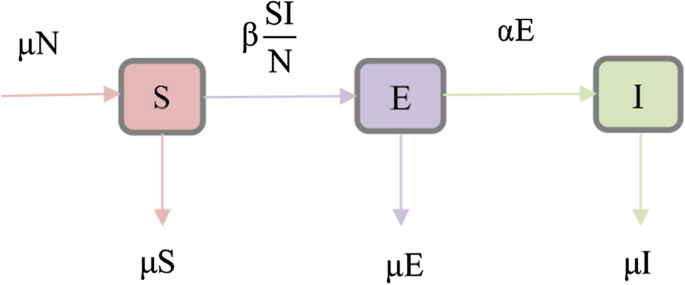
In the present work we introduced and analyzed the most basic transmission SEI (susceptible-exposed-infective) model for a directly transmitted infectious disease caused by Coronavirus disease 2019 (COVID-19). The SEI model is modeling as a Markov chain and we computed a closed form formula of the mean first passage times (MFPT’s) vector arising from non-homogeneous Markov chain random walk (NHMC-RW) on the non-negative integers. Some particular cases, which lead to a relationship between the elements of the MFPT’s vectors. An efficient algorithm applied on mathematica program for computing MFPT’s vector of the NHMC-RW is given.
使用马尔可夫链的易感-暴露-感染模型
在本研究中,我们介绍并分析了由2019年冠状病毒病(COVID-19)引起的直接传播传染病的最基本传播SEI(易感-暴露-感染)模型。SEI 模型被建模为马尔科夫链,我们计算了非均质马尔科夫链随机游走(NHMC-RW)在非负整数上产生的平均首次通过时间(MFPT's)向量的封闭式公式。一些特殊情况下,MFPT 向量元素之间的关系。给出了一种应用于计算 NHMC-RW 的 MFPT 向量的高效算法。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Nonlinear Mathematical Physics
PHYSICS, MATHEMATICAL-PHYSICS, MATHEMATICAL
CiteScore
1.60
自引率
0.00%
发文量
67
审稿时长
3 months
期刊介绍:
Journal of Nonlinear Mathematical Physics (JNMP) publishes research papers on fundamental mathematical and computational methods in mathematical physics in the form of Letters, Articles, and Review Articles.
Journal of Nonlinear Mathematical Physics is a mathematical journal devoted to the publication of research papers concerned with the description, solution, and applications of nonlinear problems in physics and mathematics.
The main subjects are:
-Nonlinear Equations of Mathematical Physics-
Quantum Algebras and Integrability-
Discrete Integrable Systems and Discrete Geometry-
Applications of Lie Group Theory and Lie Algebras-
Non-Commutative Geometry-
Super Geometry and Super Integrable System-
Integrability and Nonintegrability, Painleve Analysis-
Inverse Scattering Method-
Geometry of Soliton Equations and Applications of Twistor Theory-
Classical and Quantum Many Body Problems-
Deformation and Geometric Quantization-
Instanton, Monopoles and Gauge Theory-
Differential Geometry and Mathematical Physics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


