Strong Norm Error Bounds for Quasilinear Wave Equations Under Weak CFL-Type Conditions

IF 2.5 1区数学 Q2 COMPUTER SCIENCE, THEORY & METHODS

Foundations of Computational Mathematics Pub Date : 2024-02-13 DOI:10.1007/s10208-024-09639-w

Benjamin Dörich

引用次数: 0

Abstract

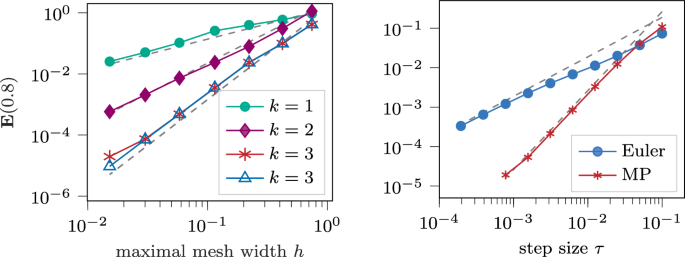
In the present paper, we consider a class of quasilinear wave equations on a smooth, bounded domain. We discretize it in space with isoparametric finite elements and apply a semi-implicit Euler and midpoint rule as well as the exponential Euler and midpoint rule to obtain four fully discrete schemes. We derive rigorous error bounds of optimal order for the semi-discretization in space and the fully discrete methods in norms which are stronger than the classical \(H^1\times L^2\) energy norm under weak CFL-type conditions. To confirm our theoretical findings, we also present numerical experiments.

Abstract Image

查看原文本刊更多论文

弱 CFL 型条件下准线性波方程的强规范误差约束

在本文中，我们考虑了光滑有界域上的一类准线性波方程。我们用等参数有限元对其进行空间离散化，并应用半隐式欧拉和中点规则以及指数式欧拉和中点规则得到四个全离散方案。我们为空间半离散化和完全离散方法推导出严格的最优阶误差边界，在弱 CFL 型条件下，其规范比经典的 \(H^1\times L^2\) 能量规范更强。为了证实我们的理论发现，我们还进行了数值实验。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Foundations of Computational Mathematics 数学-计算机：理论方法

CiteScore

6.90

自引率

3.30%

发文量

审稿时长

>12 weeks

期刊介绍： Foundations of Computational Mathematics (FoCM) will publish research and survey papers of the highest quality which further the understanding of the connections between mathematics and computation. The journal aims to promote the exploration of all fundamental issues underlying the creative tension among mathematics, computer science and application areas unencumbered by any external criteria such as the pressure for applications. The journal will thus serve an increasingly important and applicable area of mathematics. The journal hopes to further the understanding of the deep relationships between mathematical theory: analysis, topology, geometry and algebra, and the computational processes as they are evolving in tandem with the modern computer. With its distinguished editorial board selecting papers of the highest quality and interest from the international community, FoCM hopes to influence both mathematics and computation. Relevance to applications will not constitute a requirement for the publication of articles. The journal does not accept code for review however authors who have code/data related to the submission should include a weblink to the repository where the data/code is stored.