Multiplicity of topological systems

IF 0.8 3区数学 Q2 MATHEMATICS

Ergodic Theory and Dynamical Systems Pub Date : 2024-02-05 DOI:10.1017/etds.2023.118

DAVID BURGUET, RUXI SHI

引用次数: 0

Abstract

We define the topological multiplicity of an invertible topological system 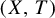Abstract Image $(X,T)$ as the minimal number k of real continuous functions $f_1,\ldots , f_k$ such that the functions 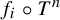$f_i\circ T^n$, 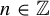$n\in {\mathbb {Z}}$, 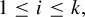$1\leq i\leq k,$ span a dense linear vector space in the space of real continuous functions on X endowed with the supremum norm. We study some properties of topological systems with finite multiplicity. After giving some examples, we investigate the multiplicity of subshifts with linear growth complexity.

查看原文本刊更多论文

拓扑系统的多重性

我们将可逆拓扑系统 $(X,T)$ 的拓扑多重性定义为实数连续函数 $f_1,\ldots , f_k$ 的最小数目 k，使得函数 $f_i\circ T^n$, $n\in {\mathbb {Z}}$, $1\leq i\leq k,$ 在 X 上的实数连续函数空间中横跨一个簇密的线性向量空间，并赋予上顶规范。我们研究具有有限多重性的拓扑系统的一些性质。在给出一些例子之后，我们研究了具有线性增长复杂性的子转移的多重性。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Ergodic Theory and Dynamical Systems 数学-数学

CiteScore

1.70

自引率

11.10%

发文量

113

审稿时长

6-12 weeks

期刊介绍： Ergodic Theory and Dynamical Systems focuses on a rich variety of research areas which, although diverse, employ as common themes global dynamical methods. The journal provides a focus for this important and flourishing area of mathematics and brings together many major contributions in the field. The journal acts as a forum for central problems of dynamical systems and of interactions of dynamical systems with areas such as differential geometry, number theory, operator algebras, celestial and statistical mechanics, and biology.