Strong consistency of tail value-at-risk estimator and corresponding general results under widely orthant dependent samples
IF 1.1
3区 数学
Q2 STATISTICS & PROBABILITY
引用次数: 0
Abstract
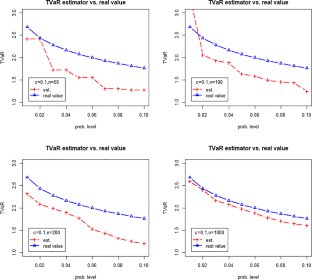
In this paper, strong consistency of tail value-at-risk (TVaR) estimator under widely orthant dependent (WOD) samples is established, and a numerical simulation is performed to verify the validity of the theoretical results. To reveal the essence of the result, theoretical discussion on complete and complete moment convergence corresponding to the Baum–Katz law, as well as the Marcinkiewicz–Zygmund type strong law of large numbers (MZSLLN) for maximal weighted sums and maximal product sums of widely orthant dependent (WOD) random variables are investigated. The results obtained in the context extend the corresponding ones for independent and some dependent random variables.
广泛正交依存样本下尾部风险价值估计器的强一致性及相应的一般结果
本文建立了广泛正交依赖(WOD)样本下尾部风险值(TVaR)估计器的强一致性,并通过数值模拟验证了理论结果的正确性。为了揭示结果的本质,研究了与 Baum-Katz 定律相对应的完全收敛和完全矩收敛,以及广泛正交依存(WOD)随机变量的最大加权和和最大乘积和的 Marcinkiewicz-Zygmund 型强大数定律(MZSLLN)。在此背景下获得的结果扩展了独立随机变量和某些从属随机变量的相应结果。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Statistical Papers
数学-统计学与概率论
CiteScore
2.80
自引率
7.70%
发文量
95
审稿时长
6-12 weeks
期刊介绍:
The journal Statistical Papers addresses itself to all persons and organizations that have to deal with statistical methods in their own field of work. It attempts to provide a forum for the presentation and critical assessment of statistical methods, in particular for the discussion of their methodological foundations as well as their potential applications. Methods that have broad applications will be preferred. However, special attention is given to those statistical methods which are relevant to the economic and social sciences. In addition to original research papers, readers will find survey articles, short notes, reports on statistical software, problem section, and book reviews.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


