Mass-growth of triangulated auto-equivalences

IF 0.5 4区数学 Q3 MATHEMATICS

Manuscripta Mathematica Pub Date : 2024-01-18 DOI:10.1007/s00229-023-01533-z

Jon Woolf

引用次数: 0

Abstract

We relate the mass growth (with respect to a stability condition) of an exact auto-equivalence of a triangulated category to the dynamical behaviour of its action on the space of stability conditions. One consequence is that this action is free and proper whenever the mass growth is non-vanishing.

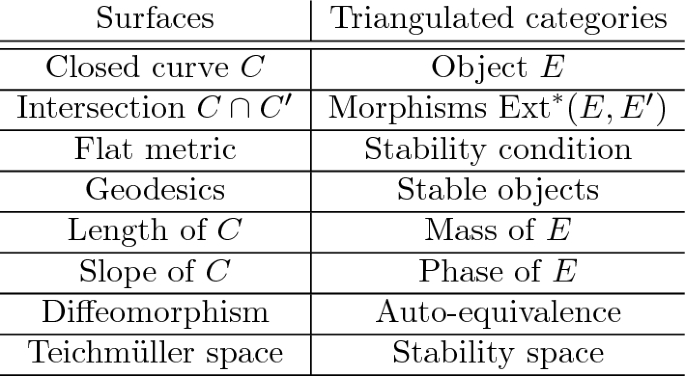
Abstract Image

查看原文本刊更多论文

三角形自等式的质量增长

我们将三角范畴精确自等价的质量增长（相对于稳定性条件）与其在稳定性条件空间上的作用的动力学行为联系起来。结果之一是，只要质量增长是非消失的，这个作用就是自由的和适当的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Manuscripta Mathematica 数学-数学

CiteScore

1.40

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： manuscripta mathematica was founded in 1969 to provide a forum for the rapid communication of advances in mathematical research. Edited by an international board whose members represent a wide spectrum of research interests, manuscripta mathematica is now recognized as a leading source of information on the latest mathematical results.