Nowhere scattered multiplier algebras

IF 1.3 3区数学 Q1 MATHEMATICS

Proceedings of the Royal Society of Edinburgh Section A-Mathematics Pub Date : 2024-01-05 DOI:10.1017/prm.2023.123

Eduard Vilalta

引用次数: 0

Abstract

We study sufficient conditions under which a nowhere scattered $\mathrm {C}^*$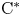 Abstract Image -algebra $A$ 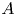has a nowhere scattered multiplier algebra $\mathcal {M}(A)$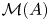, that is, we study when $\mathcal {M}(A)$ 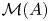has no nonzero, elementary ideal-quotients. In particular, we prove that a $\sigma$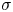-unital $\mathrm {C}^*$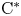-algebra $A$ 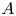of

(i) finite nuclear dimension, or
(ii) real rank zero, or
(iii) stable rank one with $k$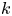-comparison,

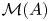is nowhere scattered if and only if $\mathcal {M}(A)$ Abstract Image

is.

查看原文本刊更多论文

无处不在的乘法代数

我们研究了一个无处分散的 $\mathrm {C}^*$ 代数 $A$ 具有一个无处分散的乘子代数 $\mathcal {M}(A)$ 的充分条件，也就是说，我们研究了 $\mathcal {M}(A)$ 没有非零的、基本的理想数的情况。特别是，我们证明，当且仅当 $\mathcal {M}(A)$ 是时，一个具有（i）有限核维度的 $\sigma$-unital $\mathrm {C}^*$-algebra $A$，或（ii）实秩为零，或（iii）具有 $k$ 比较的稳定秩一的 $\sigma$-unital $\mathrm {C}^*$-algebra $A$ 是无处分散的。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Proceedings of the Royal Society of Edinburgh Section A-Mathematics 数学-数学

CiteScore

3.00

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： A flagship publication of The Royal Society of Edinburgh, Proceedings A is a prestigious, general mathematics journal publishing peer-reviewed papers of international standard across the whole spectrum of mathematics, but with the emphasis on applied analysis and differential equations. An international journal, publishing six issues per year, Proceedings A has been publishing the highest-quality mathematical research since 1884. Recent issues have included a wealth of key contributors and considered research papers.