Mixing convergence of LSE for supercritical AR(2) processes with Gaussian innovations using random scaling
IF 0.9
4区 数学
Q3 STATISTICS & PROBABILITY
引用次数: 0
Abstract
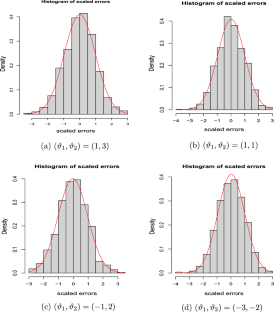
We prove mixing convergence of the least squares estimator of autoregressive parameters for supercritical autoregressive processes of order 2 with Gaussian innovations having real characteristic roots with different absolute values. We use an appropriate random scaling such that the limit distribution is a two-dimensional normal distribution concentrated on a one-dimensional ray determined by the characteristic root having the larger absolute value.
使用随机缩放对具有高斯创新的超临界 AR(2) 过程的 LSE 进行混合收敛
我们证明了具有不同绝对值实特征根的高斯创新的 2 阶超临界自回归过程的自回归参数最小二乘估计值的混合收敛性。我们使用适当的随机缩放,使得极限分布是集中在由绝对值较大的特征根所决定的一维射线上的二维正态分布。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Metrika
数学-统计学与概率论
CiteScore
1.50
自引率
14.30%
发文量
39
审稿时长
6-12 weeks
期刊介绍:
Metrika is an international journal for theoretical and applied statistics. Metrika publishes original research papers in the field of mathematical statistics and statistical methods. Great importance is attached to new developments in theoretical statistics, statistical modeling and to actual innovative applicability of the proposed statistical methods and results. Topics of interest include, without being limited to, multivariate analysis, high dimensional statistics and nonparametric statistics; categorical data analysis and latent variable models; reliability, lifetime data analysis and statistics in engineering sciences.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


