Sometimes (often?) responses to multiple stressors can be predicted from single-stressor effects: A case study using an agent-based population model of croaker in the Gulf of Mexico

Abstract

Objective

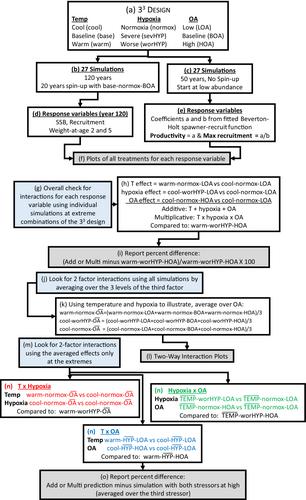
Rapid changes in the world's oceans make assessment of fish population responses to multiple stressors, especially on scales relevant to management, increasingly important. I used an existing agent-based, spatially explicit model of Atlantic Croaker Micropogonias undulatus in the northern Gulf of Mexico to examine how temperature, hypoxia, and ocean acidification, singly and in combinations, affect long-term population dynamics.

Methods

I performed a factorial simulation experiment with each stressor at three levels and analyzed various treatment combinations to assess the additivity and multiplicity of interactions. The response variables were long-term equilibrium (final year) values of spawning stock biomass (SSB), recruitment, weight at age, and two measures of stock productivity (recruits per SSB and maximum recruitment) derived from the spawner–recruit relationship fitted to model output. I used the single-stressor effects from the experiment to predict how the response variables would change when all three stressors were changed. Single-stressor effects were combined as the sum of the fractional changes (additive scale) and the product of ratios of changes (multiplicative scale) and compared to the responses in simulations with all stressors imposed.

Result

Analyzing the factorial design for two-way and three-way interactions showed that there were many interactions on the additive scale but very few on the multiplicative scale. Thus, the responses to multiple stressors were well predicted from single stressor effects when combined as multiplicative effects.

Conclusion

I discuss how the lack of strong interactions could be due to model assumptions, the structure of the model, or oversimplified representation of stressor effects. Alternatively, the model and analysis may be sufficiently realistic and weak interactions on the multiplicative scale may be common. This would reduce a complicated multi-factor situation to a series of more tractable single-factor effects. A critical next step is to determine how we can a priori identify situations of low interactions (i.e., predictable from single-stressor effects) without having to already know the multi-stressor response.