On the average time complexity of computation with random partition
IF 2.8
3区 计算机科学
Q2 COMPUTER SCIENCE, THEORY & METHODS
引用次数: 0
Abstract
Some computations are based on structures of random partition. They take an n-size problem as input, then break this problem into sub-problems of randomized size, execute calculations on each sub-problems and combine results from these calculations at last. We propose a combinatorial method for analyzing such computations and prove that the averaged time complexity is in terms of Stirling numbers of the second kind. The result shows that the average time complexity is decreased about one order of magnitude compared to that of the original solution. We also show two application cases where random partition structures are applied to improve performance.
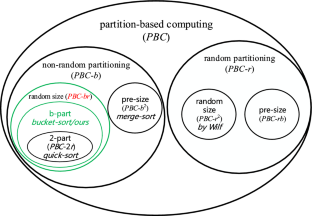
关于随机分区计算的平均时间复杂性
有些计算基于随机分区结构。它们将一个 n 大小的问题作为输入,然后将这个问题分解成随机大小的子问题,对每个子问题执行计算,最后将这些计算结果合并。我们提出了一种分析此类计算的组合方法,并证明了平均时间复杂度是以第二类斯特林数表示的。结果表明,与原始解法相比,平均时间复杂度降低了约一个数量级。我们还展示了应用随机分区结构提高性能的两个应用案例。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computing
工程技术-计算机:理论方法
CiteScore
8.20
自引率
2.70%
发文量
107
审稿时长
3 months
期刊介绍:
Computing publishes original papers, short communications and surveys on all fields of computing. The contributions should be written in English and may be of theoretical or applied nature, the essential criteria are computational relevance and systematic foundation of results.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


