On the accuracy of the finite volume approximations to nonlocal conservation laws

Abstract

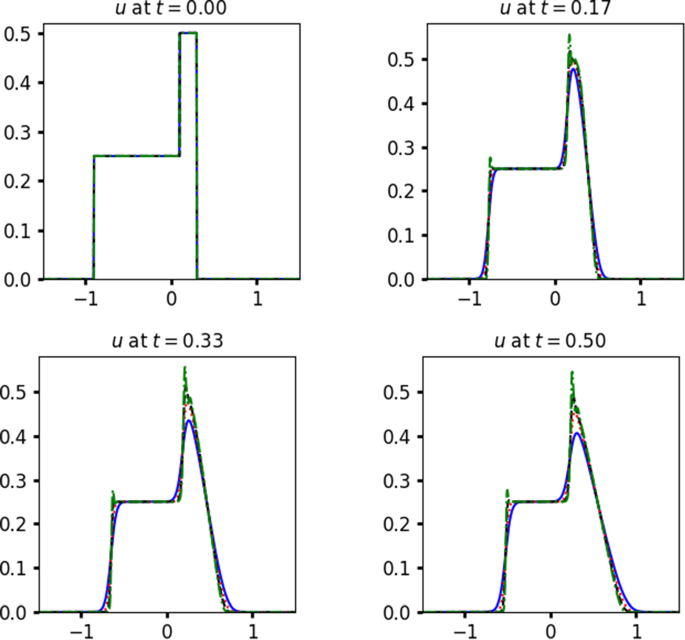
In this article, we discuss the error analysis for a certain class of monotone finite volume schemes approximating nonlocal scalar conservation laws, modeling traffic flow and crowd dynamics, without any additional assumptions on monotonicity or linearity of the kernel \(\mu \) or the flux f. We first prove a novel Kuznetsov-type lemma for this class of PDEs and thereby show that the finite volume approximations converge to the entropy solution at the rate of \(\sqrt{\Delta t}\) in \(L^1(\mathbb {R})\). To the best of our knowledge, this is the first proof of any type of convergence rate for this class of conservation laws. We also present numerical experiments to illustrate this result.