On stable commutator length of non-filling curves in surfaces

IF 1.3 3区数学 Q1 MATHEMATICS

Proceedings of the Royal Society of Edinburgh Section A-Mathematics Pub Date : 2023-12-14 DOI:10.1017/prm.2023.121

Max Forester, Justin Malestein

引用次数: 0

Abstract

We give a new proof of rationality of stable commutator length (scl) of certain elements in surface groups: those represented by curves that do not fill the surface. Such elements always admit extremal surfaces for scl. These results also hold more generally for non-filling $1$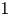 Abstract Image –chains.

查看原文本刊更多论文

论曲面非填充曲线的稳定换向器长度

给出了曲面群中某些元素的稳定换向子长度(scl)的合理性的一个新的证明:这些元素由不填满曲面的曲线表示。这样的元素总是允许scl的极值面。这些结果也适用于非填充$1$链。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Proceedings of the Royal Society of Edinburgh Section A-Mathematics 数学-数学

CiteScore

3.00

自引率

0.00%

发文量

审稿时长

6-12 weeks

期刊介绍： A flagship publication of The Royal Society of Edinburgh, Proceedings A is a prestigious, general mathematics journal publishing peer-reviewed papers of international standard across the whole spectrum of mathematics, but with the emphasis on applied analysis and differential equations. An international journal, publishing six issues per year, Proceedings A has been publishing the highest-quality mathematical research since 1884. Recent issues have included a wealth of key contributors and considered research papers.