Random and mean Lyapunov exponents for

IF 0.8 3区数学 Q2 MATHEMATICS

Ergodic Theory and Dynamical Systems Pub Date : 2023-12-11 DOI:10.1017/etds.2023.106

DIEGO ARMENTANO, GAUTAM CHINTA, SIDDHARTHA SAHI, MICHAEL SHUB

{"title":"Random and mean Lyapunov exponents for","authors":"DIEGO ARMENTANO, GAUTAM CHINTA, SIDDHARTHA SAHI, MICHAEL SHUB","doi":"10.1017/etds.2023.106","DOIUrl":null,"url":null,"abstract":"We consider orthogonally invariant probability measures on <img data-mimesubtype=\"png\" data-type=\"\" src=\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20231207140347424-0756:S0143385723001062:S0143385723001062_inline2.png\">$\\operatorname {\\mathrm {GL}}_n(\\mathbb {R})$</img> and compare the mean of the logs of the moduli of eigenvalues of the matrices with the Lyapunov exponents of random matrix products independently drawn with respect to the measure. We give a lower bound for the former in terms of the latter. The results are motivated by Dedieu and Shub [On random and mean exponents for unitarily invariant probability measures on <img data-mimesubtype=\"png\" data-type=\"\" src=\"https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20231207140347424-0756:S0143385723001062:S0143385723001062_inline3.png\">$\\operatorname {\\mathrm {GL}}_n(\\mathbb {C})$</img>. Astérisque 287 (2003), xvii, 1–18]. A novel feature of our treatment is the use of the theory of spherical polynomials in the proof of our main result.","PeriodicalId":50504,"journal":{"name":"Ergodic Theory and Dynamical Systems","volume":null,"pages":null},"PeriodicalIF":0.8000,"publicationDate":"2023-12-11","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Ergodic Theory and Dynamical Systems","FirstCategoryId":"100","ListUrlMain":"https://doi.org/10.1017/etds.2023.106","RegionNum":3,"RegionCategory":"数学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q2","JCRName":"MATHEMATICS","Score":null,"Total":0}

引用次数: 0

Abstract

We consider orthogonally invariant probability measures on 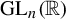Abstract Image $\operatorname {\mathrm {GL}}_n(\mathbb {R})$ and compare the mean of the logs of the moduli of eigenvalues of the matrices with the Lyapunov exponents of random matrix products independently drawn with respect to the measure. We give a lower bound for the former in terms of the latter. The results are motivated by Dedieu and Shub [On random and mean exponents for unitarily invariant probability measures on 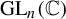Abstract Image $\operatorname {\mathrm {GL}}_n(\mathbb {C})$. Astérisque 287 (2003), xvii, 1–18]. A novel feature of our treatment is the use of the theory of spherical polynomials in the proof of our main result.

查看原文本刊更多论文

的随机和平均李亚普诺夫指数

我们考虑了$\operatorname {\mathrm {GL}}_n(\mathbb {R})$上的正交不变概率度量，并比较了矩阵特征值对数的均值与随机矩阵乘积的李雅普诺夫指数，随机矩阵乘积是相对于度量独立抽取的。我们用后者给出了前者的下限。这些结果来自 Dedieu 和 Shub [On random and mean exponents for unitarily invariant probability measures on $\operatorname {\mathrm {GL}}_n(\mathbb {C})$.Astérisque 287 (2003), xvii, 1-18].我们的处理方法的一个新特点是在证明我们的主要结果时使用了球面多项式理论。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Ergodic Theory and Dynamical Systems 数学-数学

CiteScore

1.70

自引率

11.10%

发文量

113

审稿时长

6-12 weeks

期刊介绍： Ergodic Theory and Dynamical Systems focuses on a rich variety of research areas which, although diverse, employ as common themes global dynamical methods. The journal provides a focus for this important and flourishing area of mathematics and brings together many major contributions in the field. The journal acts as a forum for central problems of dynamical systems and of interactions of dynamical systems with areas such as differential geometry, number theory, operator algebras, celestial and statistical mechanics, and biology.