Most numbers are not normal
IF 0.8
3区 数学
Q3 MATHEMATICS
Mathematical Proceedings of the Cambridge Philosophical Society
Pub Date : 2022-11-28
DOI:10.1017/s0305004122000469
引用次数: 0
Abstract
We show, from a topological viewpoint, that most numbers are not normal in a strong sense. More precisely, the set of numbers
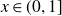 $x \in (0,1]$
with the following property is comeager: for all integers
$x \in (0,1]$
with the following property is comeager: for all integers
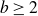 $b\ge 2$
and
$b\ge 2$
and
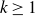 $k\ge 1$
, the sequence of vectors made by the frequencies of all possibile strings of length k in the b-adic representation of x has a maximal subset of accumulation points, and each of them is the limit of a subsequence with an index set of nonzero asymptotic density. This extends and provides a streamlined proof of the main result given by Olsen (2004) in this Journal. We provide analogues in the context of analytic P-ideals and regular matrices.
$k\ge 1$
, the sequence of vectors made by the frequencies of all possibile strings of length k in the b-adic representation of x has a maximal subset of accumulation points, and each of them is the limit of a subsequence with an index set of nonzero asymptotic density. This extends and provides a streamlined proof of the main result given by Olsen (2004) in this Journal. We provide analogues in the context of analytic P-ideals and regular matrices.
大多数数字都不正常
我们从拓扑学的观点证明,大多数数在强意义上是不正常的。更准确地说,具有以下性质的数字集$x \in(0,1]$是可聚的:对于所有整数$b\ge 2$和$k\ge 1$,由x的b进表示中长度为k的所有可能字符串的频率组成的向量序列有一个最大的累加点子集,并且每个累加点都是具有非零渐近密度索引集的子序列的极限。这扩展并提供了Olsen(2004)在本刊中给出的主要结果的简化证明。我们在解析p理想和正则矩阵的背景下提供类似物。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
1.70
自引率
0.00%
发文量
39
审稿时长
6-12 weeks
期刊介绍:
Papers which advance knowledge of mathematics, either pure or applied, will be considered by the Editorial Committee. The work must be original and not submitted to another journal.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


