The anisotropic min-max theory: Existence of anisotropic minimal and CMC surfaces
IF 2.7
1区 数学
Q1 MATHEMATICS
引用次数: 0
Abstract
We prove the existence of nontrivial closed surfaces with constant anisotropic mean curvature with respect to elliptic integrands in closed smooth –dimensional Riemannian manifolds. The constructed min-max surfaces are smooth with at most one singular point. The constant anisotropic mean curvature can be fixed to be any real number. In particular, we partially solve a conjecture of Allard in dimension .
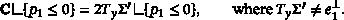
各向异性最小-最大理论:各向异性极小面和CMC面的存在性
我们证明了闭光滑三维黎曼流形中的椭圆积分具有恒定各向异性平均曲率的非平凡闭曲面的存在性。构造的最小-最大曲面是光滑的,最多有一个奇点。恒定各向异性平均曲率可以固定为任意实数。特别地,我们部分地解决了Allard在三维空间中的一个猜想。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
6.70
自引率
3.30%
发文量
59
审稿时长
>12 weeks
期刊介绍:
Communications on Pure and Applied Mathematics (ISSN 0010-3640) is published monthly, one volume per year, by John Wiley & Sons, Inc. © 2019.
The journal primarily publishes papers originating at or solicited by the Courant Institute of Mathematical Sciences. It features recent developments in applied mathematics, mathematical physics, and mathematical analysis. The topics include partial differential equations, computer science, and applied mathematics. CPAM is devoted to mathematical contributions to the sciences; both theoretical and applied papers, of original or expository type, are included.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


