Optimal Control Selection for Stabilizing the Inverted Pendulum Problem Using Neural Network Method

IF 1 Q4 OPTICS

Optical Memory and Neural Networks Pub Date : 2023-11-28 DOI:10.3103/S1060992X23060115

D. A. Tarkhov, D. A. Lavygin, O. A. Skripkin, M. D. Zakirova, T. V. Lazovskaya

引用次数: 0

Abstract

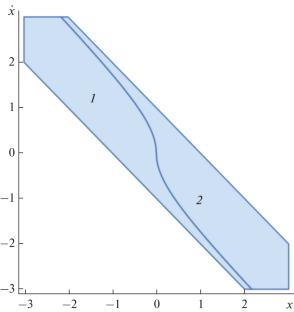
The task of managing unstable systems is a critically important management problem, as an unstable object can pose significant danger to humans and the environment when it fails. In this paper, a neural network was trained to determine the optimal control for an unstable system, based on a comparative analysis of two control methods: the implicit Euler method and the linearization method. This neural network identifies the optimal control based on the position of a point on the phase plane.

Abstract Image

查看原文本刊更多论文

用神经网络方法稳定倒立摆问题的最优控制选择

管理不稳定系统的任务是一个非常重要的管理问题，因为不稳定的对象在发生故障时可能对人类和环境造成重大危险。本文在比较分析隐式欧拉法和线性化法两种控制方法的基础上，训练神经网络来确定不稳定系统的最优控制。该神经网络基于点在相位平面上的位置来识别最优控制。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Optical Memory and Neural Networks OPTICS-

CiteScore

1.50

自引率

11.10%

发文量

期刊介绍： The journal covers a wide range of issues in information optics such as optical memory, mechanisms for optical data recording and processing, photosensitive materials, optical, optoelectronic and holographic nanostructures, and many other related topics. Papers on memory systems using holographic and biological structures and concepts of brain operation are also included. The journal pays particular attention to research in the field of neural net systems that may lead to a new generation of computional technologies by endowing them with intelligence.