General Soliton and (Semi-)Rational Solutions of a (2+1)-Dimensional Sinh-Gordon Equation
IF 1.4
4区 物理与天体物理
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
Abstract In this paper, we investigate solutions of a (2+1)-dimensional sinh-Gordon equation. General solitons and (semi-)rational solutions are derived by the combination of Hirota’s bilinear method and Kadomtsev-Petviashvili hierarchy reduction approach. General solutions are expressed as $$N\times N$$
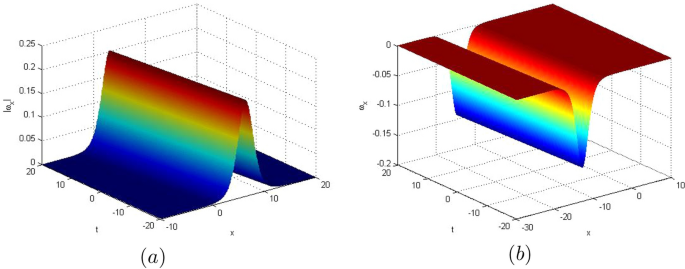
一类(2+1)维Sinh-Gordon方程的一般孤子解和(半)有理解
摘要本文研究了一类(2+1)维sinh-Gordon方程的解。结合Hirota的双线性方法和Kadomtsev-Petviashvili层次约简方法,导出了一般孤子和(半)有理解。通解表示为$$N\times N$$ N × N gram型行列式。当行列式大小N为偶数时,我们生成位于恒定背景上的孤子、线呼吸子和(半)有理解。特别地,我们通过渐近分析证明了孤子的碰撞是完全弹性的。当N为奇数时,我们得到周期背景下的精确解。用图表分析了这些解的动力学行为。对于有理解,我们展示了块的相互作用。对于半有理解,我们找到了块与孤子之间的相互作用解。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Nonlinear Mathematical Physics
PHYSICS, MATHEMATICAL-PHYSICS, MATHEMATICAL
CiteScore
1.60
自引率
0.00%
发文量
67
审稿时长
3 months
期刊介绍:
Journal of Nonlinear Mathematical Physics (JNMP) publishes research papers on fundamental mathematical and computational methods in mathematical physics in the form of Letters, Articles, and Review Articles.
Journal of Nonlinear Mathematical Physics is a mathematical journal devoted to the publication of research papers concerned with the description, solution, and applications of nonlinear problems in physics and mathematics.
The main subjects are:
-Nonlinear Equations of Mathematical Physics-
Quantum Algebras and Integrability-
Discrete Integrable Systems and Discrete Geometry-
Applications of Lie Group Theory and Lie Algebras-
Non-Commutative Geometry-
Super Geometry and Super Integrable System-
Integrability and Nonintegrability, Painleve Analysis-
Inverse Scattering Method-
Geometry of Soliton Equations and Applications of Twistor Theory-
Classical and Quantum Many Body Problems-
Deformation and Geometric Quantization-
Instanton, Monopoles and Gauge Theory-
Differential Geometry and Mathematical Physics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


