Gradient descent-based freeform optics design for illumination using algorithmic differentiable non-sequential ray tracing

Abstract

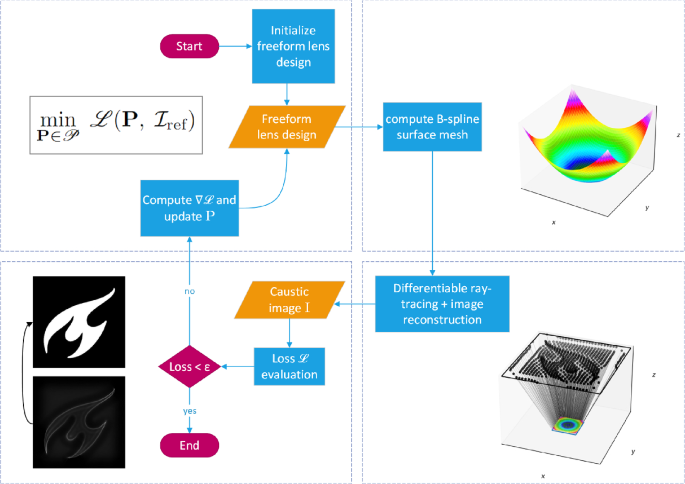
Abstract Algorithmic differentiable ray tracing is a new paradigm that allows one to solve the forward problem of how light propagates through an optical system while obtaining gradients of the simulation results with respect to parameters specifying the optical system. Specifically, the use of algorithmically differentiable non-sequential ray tracing provides an opportunity in the field of illumination engineering to design complex optical system. We demonstrate its potential by designing freeform lenses that project a prescribed irradiance distribution onto a plane. The challenge consists in finding a suitable surface geometry of the lens so that the light emitted by a light source is redistributed into a desired irradiance distribution. We discuss the crucial steps allowing the non-sequential ray tracer to be differentiable. The obtained gradients are used to optimize the geometry of the freeform, and we investigate the effectiveness of adding a multi-layer perceptron neural network to the optimization that outputs parameters defining the freeform lens. Lenses are designed for various sources such as collimated beams or point sources, and finally, a grid of point sources approximating an extended source. The obtained lens designs are finally validated using the commercial non-sequential ray tracer LightTools.