Dependence in constrained Bayesian optimization
IF 1.1
4区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
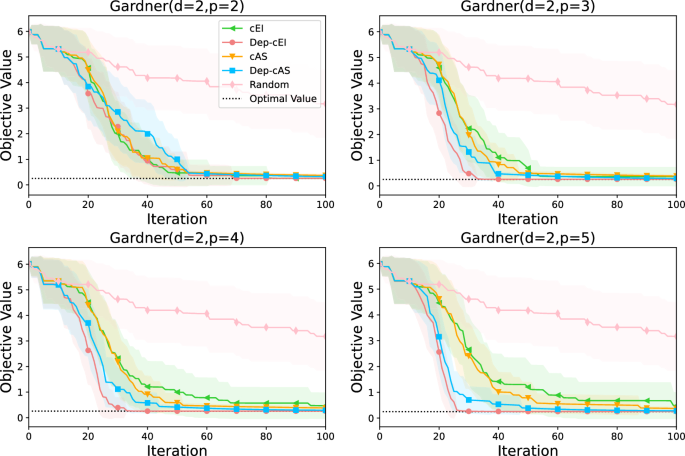
Abstract Constrained Bayesian optimization optimizes a black-box objective function subject to black-box constraints. For simplicity, most existing works assume that multiple constraints are independent. To ask, when and how does dependence between constraints help? , we remove this assumption and implement probability of feasibility with dependence (Dep-PoF) by applying multiple output Gaussian processes (MOGPs) as surrogate models and using expectation propagation to approximate the probabilities. We compare Dep-PoF and the independent version PoF. We propose two new acquisition functions incorporating Dep-PoF and test them on synthetic and practical benchmarks. Our results are largely negative: incorporating dependence between the constraints does not help much. Empirically, incorporating dependence between constraints may be useful if: (i) the solution is on the boundary of the feasible region(s) or (ii) the feasible set is very small. When these conditions are satisfied, the predictive covariance matrix from the MOGP may be poorly approximated by a diagonal matrix and the off-diagonal matrix elements may become important. Dep-PoF may apply to settings where (i) the constraints and their dependence are totally unknown and (ii) experiments are so expensive that any slightly better Bayesian optimization procedure is preferred. But, in most cases, Dep-PoF is indistinguishable from PoF.
约束贝叶斯优化中的相关性
约束贝叶斯优化是对受黑箱约束的黑箱目标函数进行优化。为简单起见,大多数现有的工作都假定多个约束是独立的。要问,约束之间的依赖何时以及如何起作用?,我们消除了这一假设,并通过将多输出高斯过程(mogp)作为代理模型,并使用期望传播来近似概率,实现了具有相关性的可行性概率(deep - pof)。我们比较了deep -PoF和独立版本的PoF。我们提出了两个包含deep - pof的新采集函数,并在综合和实际基准上进行了测试。我们的结果在很大程度上是负面的:合并约束之间的依赖并没有多大帮助。从经验上讲,如果:(i)解在可行域的边界上,或者(ii)可行集非常小,那么结合约束之间的依赖可能是有用的。当满足这些条件时,MOGP的预测协方差矩阵可能难以用对角矩阵近似,而非对角矩阵元素可能变得重要。deep - pof可能适用于以下情况:(i)约束条件及其依赖性完全未知;(ii)实验成本太高,任何稍好一点的贝叶斯优化过程都是首选。但是,在大多数情况下,deep -PoF与PoF难以区分。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Optimization Letters
管理科学-应用数学
CiteScore
3.40
自引率
6.20%
发文量
116
审稿时长
9 months
期刊介绍:
Optimization Letters is an international journal covering all aspects of optimization, including theory, algorithms, computational studies, and applications, and providing an outlet for rapid publication of short communications in the field. Originality, significance, quality and clarity are the essential criteria for choosing the material to be published.
Optimization Letters has been expanding in all directions at an astonishing rate during the last few decades. New algorithmic and theoretical techniques have been developed, the diffusion into other disciplines has proceeded at a rapid pace, and our knowledge of all aspects of the field has grown even more profound. At the same time one of the most striking trends in optimization is the constantly increasing interdisciplinary nature of the field.
Optimization Letters aims to communicate in a timely fashion all recent developments in optimization with concise short articles (limited to a total of ten journal pages). Such concise articles will be easily accessible by readers working in any aspects of optimization and wish to be informed of recent developments.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


