Stability and dynamics of a stochastic discrete fractional-order chaotic system with short memory

Abstract

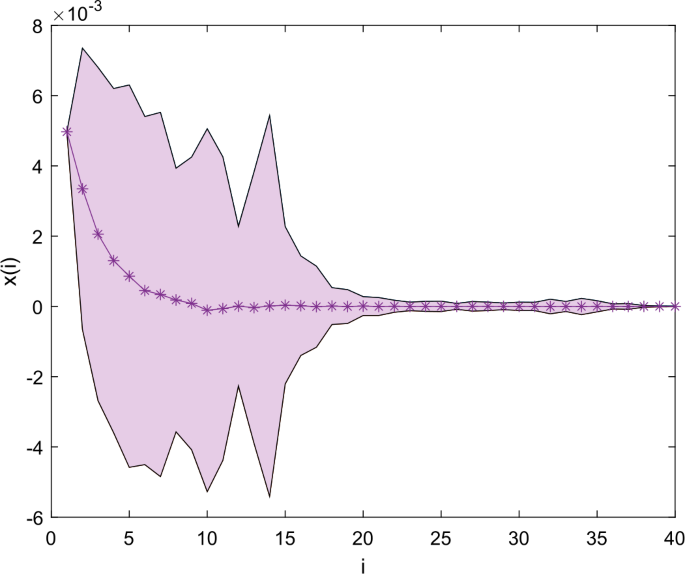
Abstract In this paper, a stochastic discrete fractional-order chaotic system with short memory is proposed, which possesses two equilibrium points. With the help of the Lyapunov function theory, some sufficient conditions for the stability in probability of the two equilibrium points are given. Secondly, the effects of fractional order and memory steps on the stability of the system are discussed. Finally, the path dynamical behavior of the system is investigated using numerical methods such as Lyapunov exponents, bifurcation diagram, phase diagram, and 0–1 test. The numerical simulation results validate the findings.