Forward invariant set preservation in discrete dynamical systems and numerical schemes for ODEs: application in biosciences

Abstract

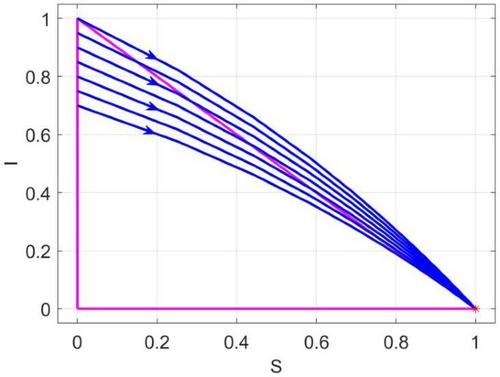
Abstract We present two results on the analysis of discrete dynamical systems and finite difference discretizations of continuous dynamical systems, which preserve their dynamics and essential properties. The first result provides a sufficient condition for forward invariance of a set under discrete dynamical systems of specific type, namely time-reversible ones. The condition involves only the boundary of the set. It is a discrete analog of the widely used tangent condition for continuous systems ( viz. the vector field points either inwards or is tangent to the boundary of the set). The second result is nonstandard finite difference (NSFD) scheme for dynamical systems defined by systems of ordinary differential equations. The NSFD scheme preserves the hyperbolic equilibria of the continuous system as well as their stability. Further, the scheme is time reversible and, through the first result, inherits from the continuous model the forward invariance of the domain. We show that the scheme is of second order, thereby solving a pending problem on the construction of higher-order nonstandard schemes without spurious solutions. It is shown that the new scheme applies directly for mass action-based models of biological and chemical processes. The application of these results, including some numerical simulations for invariant sets, is exemplified on a general Susceptible-Infective-Recovered/Removed (SIR)-type epidemiological model, which may have arbitrary large number of infective or recovered/removed compartments.