A study of progressive hedging for stochastic integer programming
IF 1.6
2区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 1
Abstract
Abstract Motivated by recent literature demonstrating the surprising effectiveness of the heuristic application of progressive hedging (PH) to stochastic mixed-integer programming (SMIP) problems, we provide theoretical support for the inclusion of integer variables, bridging the gap between theory and practice. We provide greater insight into the following observed phenomena of PH as applied to SMIP where optimal or at least feasible convergence is observed. We provide an analysis of a modified PH algorithm from a different viewpoint, drawing on the interleaving of (split) proximal-point methods (including PH), Gauss–Seidel methods, and the utilisation of variational analysis tools. Through this analysis, we show that under mild conditions, convergence to a feasible solution should be expected. In terms of convergence analysis, we provide two main contributions. First, we contribute insight into the convergence of proximal-point-like methods in the presence of integer variables via the introduction of the notion of persistent local minima. Secondly, we contribute an enhanced Gauss–Seidel convergence analysis that accommodates the variation of the objective function under mild assumptions. We provide a practical implementation of a modified PH and demonstrate its convergent behaviour with computational experiments in line with the provided analysis.
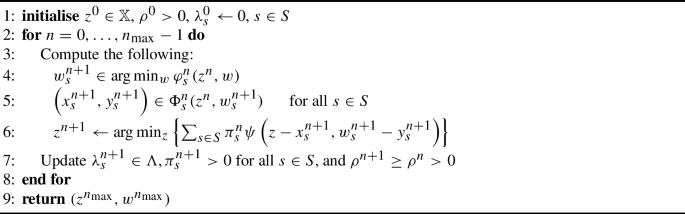
随机整数规划的渐进式套期保值研究
最近的文献证明了渐进式对冲(PH)在随机混合整数规划(SMIP)问题上的启发式应用的惊人有效性,我们为整数变量的包含提供了理论支持,弥合了理论与实践之间的差距。我们对应用于SMIP的PH观察到的以下现象提供了更深入的了解,其中观察到最优或至少可行的收敛。我们从不同的角度分析了一种改进的PH算法,利用(分裂)近点方法(包括PH),高斯-塞德尔方法和变分分析工具的利用。通过这一分析,我们表明,在温和的条件下,收敛到可行解是可以预期的。在收敛分析方面,我们提供了两个主要贡献。首先,通过引入持续局部极小值的概念,我们深入了解了在整数变量存在下近似点方法的收敛性。其次,我们提出了一个增强的Gauss-Seidel收敛分析,以适应目标函数在温和假设下的变化。我们提供了一个修改PH的实际实现,并通过计算实验证明其收敛行为与所提供的分析一致。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.70
自引率
9.10%
发文量
91
审稿时长
10 months
期刊介绍:
Computational Optimization and Applications is a peer reviewed journal that is committed to timely publication of research and tutorial papers on the analysis and development of computational algorithms and modeling technology for optimization. Algorithms either for general classes of optimization problems or for more specific applied problems are of interest. Stochastic algorithms as well as deterministic algorithms will be considered. Papers that can provide both theoretical analysis, along with carefully designed computational experiments, are particularly welcome.
Topics of interest include, but are not limited to the following:
Large Scale Optimization,
Unconstrained Optimization,
Linear Programming,
Quadratic Programming Complementarity Problems, and Variational Inequalities,
Constrained Optimization,
Nondifferentiable Optimization,
Integer Programming,
Combinatorial Optimization,
Stochastic Optimization,
Multiobjective Optimization,
Network Optimization,
Complexity Theory,
Approximations and Error Analysis,
Parametric Programming and Sensitivity Analysis,
Parallel Computing, Distributed Computing, and Vector Processing,
Software, Benchmarks, Numerical Experimentation and Comparisons,
Modelling Languages and Systems for Optimization,
Automatic Differentiation,
Applications in Engineering, Finance, Optimal Control, Optimal Design, Operations Research,
Transportation, Economics, Communications, Manufacturing, and Management Science.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


