Orthogonal ring patterns in the plane
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 0
Abstract
Abstract We introduce orthogonal ring patterns consisting of pairs of concentric circles generalizing circle patterns. We show that orthogonal ring patterns are governed by the same equation as circle patterns. For every ring pattern there exists a one parameter family of patterns that interpolates between a circle pattern and its dual. We construct ring patterns analogues of the Doyle spiral, Erf and $$z^\alpha $$
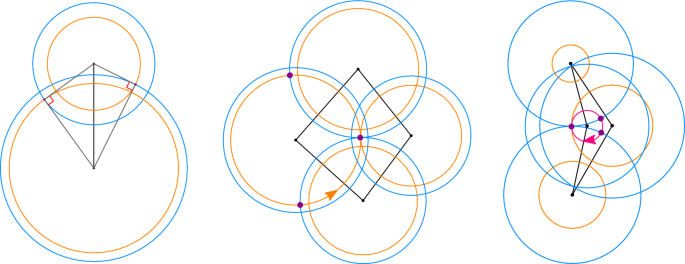
平面上的正交环形图案
摘要推广圆图案,引入由同心圆对组成的正交环图案。我们证明正交环形图案与圆形图案由相同的方程控制。对于每一个环状图案,都存在一个参数族的图案,它插在圆形图案和它的对偶图案之间。我们构造了类似Doyle螺旋、Erf和$$z^\alpha $$ z α函数的环状图案。我们还推导了基于Dirichlet和Neumann边界条件的变分原理并计算了环图案。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Geometriae Dedicata
数学-数学
CiteScore
0.90
自引率
0.00%
发文量
78
审稿时长
4-8 weeks
期刊介绍:
Geometriae Dedicata concentrates on geometry and its relationship to topology, group theory and the theory of dynamical systems.
Geometriae Dedicata aims to be a vehicle for excellent publications in geometry and related areas. Features of the journal will include:
A fast turn-around time for articles.
Special issues centered on specific topics.
All submitted papers should include some explanation of the context of the main results.
Geometriae Dedicata was founded in 1972 on the initiative of Hans Freudenthal in Utrecht, the Netherlands, who viewed geometry as a method rather than as a field. The present Board of Editors tries to continue in this spirit. The steady growth of the journal since its foundation is witness to the validity of the founder''s vision and to the success of the Editors'' mission.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


