Conservative Fourier spectral method for a class of modified Zakharov system with high-order space fractional quantum correction
IF 1.8
Q1 MATHEMATICS
引用次数: 0
Abstract
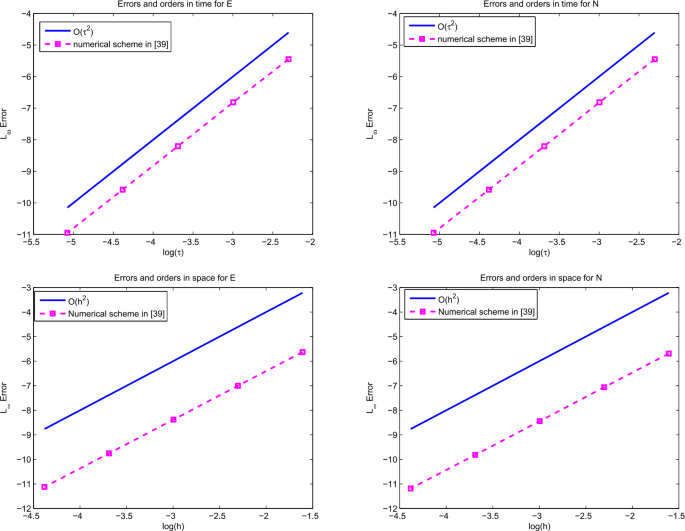
Abstract In this paper, we consider the Fourier spectral method and numerical investigation for a class of modified Zakharov system with high-order space fractional quantum correction. First, the numerical scheme of the system is developed with periodic boundary condition based on the Crank–Nicolson/leap-frog methods in time and the Fourier spectral method in space. Moreover, it is shown that the scheme preserves simultaneously mass and energy conservation laws. Second, we analyze stability and convergence of the numerical scheme. Last, the numerical experiments are given, and the results show the correctness of theoretical results and the efficiency of the conservative scheme.
一类具有高阶空间分数量子校正的修正Zakharov系统的保守傅里叶谱方法
本文研究了一类具有高阶空间分数阶量子校正的修正Zakharov系统的傅里叶谱方法和数值研究。首先,基于时间上的Crank-Nicolson /leap-frog方法和空间上的傅立叶谱方法,在周期边界条件下建立了系统的数值格式。此外,还证明了该方案同时保持了质量和能量守恒定律。其次,分析了数值格式的稳定性和收敛性。最后进行了数值实验,结果表明了理论结果的正确性和保守格式的有效性。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


