Two-step inertial forward–reflected–anchored–backward splitting algorithm for solving monotone inclusion problems
IF 2.5
3区 数学
Q1 MATHEMATICS, APPLIED
引用次数: 0
Abstract
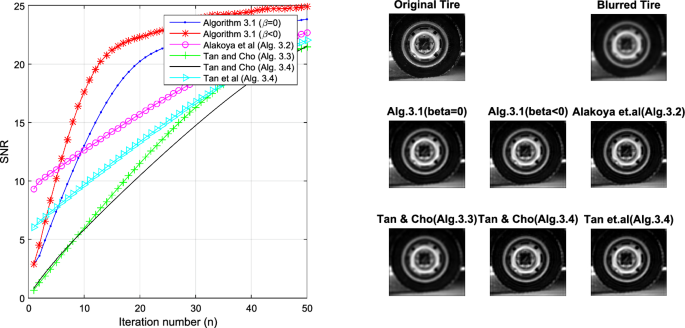
Abstract The main purpose of this paper is to propose and study a two-step inertial anchored version of the forward–reflected–backward splitting algorithm of Malitsky and Tam in a real Hilbert space. Our proposed algorithm converges strongly to a zero of the sum of a set-valued maximal monotone operator and a single-valued monotone Lipschitz continuous operator. It involves only one forward evaluation of the single-valued operator and one backward evaluation of the set-valued operator at each iteration; a feature that is absent in many other available strongly convergent splitting methods in the literature. Finally, we perform numerical experiments involving image restoration problem and compare our algorithm with known related strongly convergent splitting algorithms in the literature.
求解单调包含问题的两步惯性前反射-锚定-后向分裂算法
摘要本文的主要目的是提出并研究实Hilbert空间中Malitsky和Tam的前向反射-后向分裂算法的两步惯性锚定版本。该算法强收敛于集值极大单调算子和单值单调Lipschitz连续算子的和的零点。它在每次迭代中只涉及单值操作符的一次前向求值和集值操作符的一次后向求值;这是文献中许多其他可用的强收敛分裂方法所没有的特征。最后,我们进行了涉及图像恢复问题的数值实验,并将我们的算法与文献中已知的相关强收敛分裂算法进行了比较。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computational & Applied Mathematics
Mathematics-Computational Mathematics
CiteScore
4.50
自引率
11.50%
发文量
352
审稿时长
>12 weeks
期刊介绍:
Computational & Applied Mathematics began to be published in 1981. This journal was conceived as the main scientific publication of SBMAC (Brazilian Society of Computational and Applied Mathematics).
The objective of the journal is the publication of original research in Applied and Computational Mathematics, with interfaces in Physics, Engineering, Chemistry, Biology, Operations Research, Statistics, Social Sciences and Economy. The journal has the usual quality standards of scientific international journals and we aim high level of contributions in terms of originality, depth and relevance.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


