Hybrid Neural Network - Variational Data Assimilation algorithm to infer river discharges from SWOT-like data
IF 2
3区 地球科学
Q3 COMPUTER SCIENCE, INTERDISCIPLINARY APPLICATIONS
引用次数: 5
Abstract
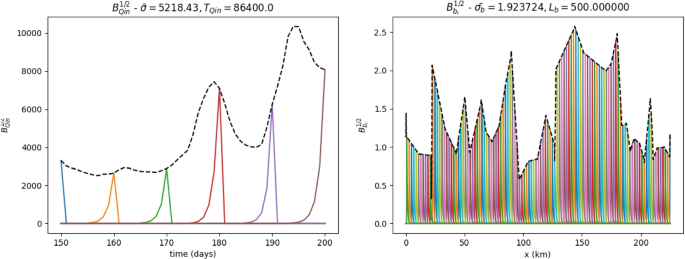
Estimating discharges Q(x, t) from altimetric measurements only, for ungauged rivers (in particular, those with unknown bathymetry b(x)), is an ill-posed inverse problem. We develop here an algorithm to estimate Q(x, t) without prior flow information other than global open datasets. Additionally, the ill-posedness feature of this inverse problem is re-investigated. Inversions based on a Variational Data Assimilation (VDA) approach enable accurate estimation of spatio-temporal variations of the discharge, but with a bias scaling the overall estimate. This key issue, which was already highlighted in our previous studies, is partly solved by considering additional hydrological information (the drainage area, $$A\ (km^2)$$ ) combined with a Machine Learning (ML) technique. Purely data-driven estimations obtained from an Artificial Neural Network (ANN) provide a reasonably good estimation at a large scale ( $$\approx 10^3$$ m). This first estimation is then employed to define the first guess of an iterative VDA algorithm. The latter relies on the Saint-Venant flow model and aims to compute the complete unknowns (discharge Q(x, t), bathymetry b(x), friction coefficient K(x, t)) at a fine scale (approximately $$10^2$$ m). The resulting complete inversion algorithm is called the H2iVDI algorithm for "Hybrid Hierarchical Variational Discharge Inference". Numerical experiments have been analyzed for 29 heterogeneous worldwide river portions. The obtained estimations present an overall bias (less than 30% for rivers with similar characteristics than those used for calibration) smaller than previous results, with accurate spatio-temporal variations of the flow. After a learning period of the observed rivers (e.g. one year), the algorithm provides two complementary estimators: a dynamic flow model enabling estimations at a fine scale and spatio-temporal extrapolations, and a low complexity estimator (based on a dedicated algebraic low Froude flow model). This last estimator provides reasonably accurate estimations (less than 30% for considered rivers) at a large scale from newly acquired WS measurements in real-time, therefore making it a potentially operational algorithm.
混合神经网络-变分数据同化算法从类似swt的数据推断河流流量
仅从高程测量中估计流量Q(x, t),对于未测量的河流(特别是那些具有未知水深b(x)的河流),是一个不适定逆问题。我们在这里开发了一种算法来估计Q(x, t),而不需要除全局开放数据集以外的先验流信息。此外,还研究了该逆问题的病态性。基于变分数据同化(VDA)方法的反演能够准确估计流量的时空变化,但总体估计存在偏差。我们之前的研究已经强调了这个关键问题,通过考虑额外的水文信息(流域面积,$$A\ (km^2)$$)和机器学习(ML)技术,可以部分解决这个问题。从人工神经网络(ANN)获得的纯数据驱动估计在大尺度上提供了相当好的估计($$\approx 10^3$$ m)。然后使用该第一次估计来定义迭代VDA算法的第一次猜测。后者依赖于Saint-Venant流动模型,旨在计算精细尺度(近似$$10^2$$ m)下的完全未知数(流量Q(x, t)、水深b(x)、摩擦系数K(x, t)),得到的完全反演算法称为“Hybrid Hierarchical Variational discharge Inference”的H2iVDI算法。对全球29条非均质河段进行了数值试验分析。获得的估计呈现出总体偏差(小于30)% for rivers with similar characteristics than those used for calibration) smaller than previous results, with accurate spatio-temporal variations of the flow. After a learning period of the observed rivers (e.g. one year), the algorithm provides two complementary estimators: a dynamic flow model enabling estimations at a fine scale and spatio-temporal extrapolations, and a low complexity estimator (based on a dedicated algebraic low Froude flow model). This last estimator provides reasonably accurate estimations (less than 30% for considered rivers) at a large scale from newly acquired WS measurements in real-time, therefore making it a potentially operational algorithm.
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Computational Geosciences
地学-地球科学综合
CiteScore
6.10
自引率
4.00%
发文量
63
审稿时长
6-12 weeks
期刊介绍:
Computational Geosciences publishes high quality papers on mathematical modeling, simulation, numerical analysis, and other computational aspects of the geosciences. In particular the journal is focused on advanced numerical methods for the simulation of subsurface flow and transport, and associated aspects such as discretization, gridding, upscaling, optimization, data assimilation, uncertainty assessment, and high performance parallel and grid computing.
Papers treating similar topics but with applications to other fields in the geosciences, such as geomechanics, geophysics, oceanography, or meteorology, will also be considered.
The journal provides a platform for interaction and multidisciplinary collaboration among diverse scientific groups, from both academia and industry, which share an interest in developing mathematical models and efficient algorithms for solving them, such as mathematicians, engineers, chemists, physicists, and geoscientists.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


