High-order spectral collocation method using tempered fractional Sturm–Liouville eigenproblems

Abstract

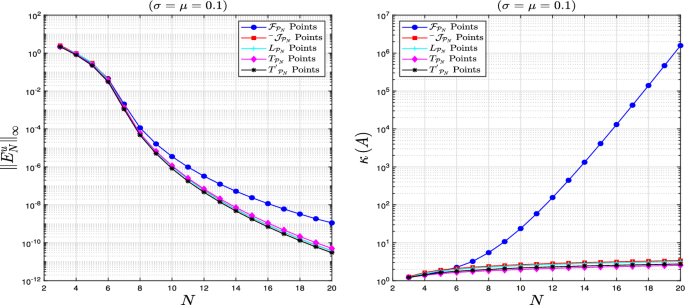
Abstract This paper presents an accurate exponential tempered fractional spectral collocation method (TFSCM) to solve one-dimensional and time-dependent tempered fractional partial differential equations (TFPDEs). We use a family of tempered fractional Sturm–Liouville eigenproblems (TFSLP) as a basis and the fractional Lagrange interpolants (FLIs) that generally satisfy the Kronecker delta (KD) function at the employed collocation points. Firstly, we drive the corresponding tempered fractional differentiation matrices (TFDMs). Then, we treat with various linear and nonlinear TFPDEs, among them, the space-tempered fractional advection and diffusion problem, the time-space tempered fractional advection–diffusion problem (TFADP), the multi-term time-space tempered fractional problems, and the time-space tempered fractional Burgers’ equation (TFBE) to investigate the numerical capability of the fractional collocation method. The study includes a numerical examination of the produced condition number $$\kappa (A)$$ κ ( A ) of the linear systems. The accuracy and efficiency of the proposed method are studied from the standpoint of the $$L^\infty $$ L ∞ -norm error and exponential rate of spectral convergence.