Evaluating the Impacts of Thermal Conductivity on Casson Fluid Flow Near a Slippery Sheet: Numerical Simulation Using Sixth-Kind Chebyshev Polynomials

Abstract

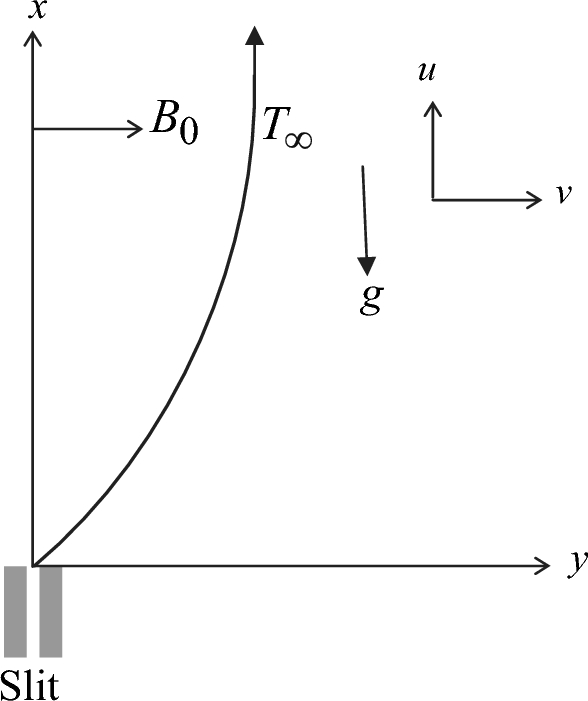
Abstract This study aims to elucidates the effects of Ohmic dissipation and the magnetic field on the behavior of a Casson fluid flowing across a vertically stretched surface. The goal is to solve the problem by using numerical approaches. Furthermore, the fluid’s thermal conductivity is intended to vary proportionately with temperature. The effects of thermal radiation, electric fields, and viscous dissipation are taken into account in this study. A set of partial differential equations (PDEs) is used to quantitatively reflect the numerous physical conditions that are placed on the sheet’s surrounding wall as well as the processes of momentum and heat transport. A system of ordinary differential equations (ODEs) is created from the set of PDEs by using similarity transformations. The mathematical model of the problem is made easier by this conversion. Furthermore, this study’s main goal is to investigate the numerical treatment of the proposed model that takes Caputo fractional-order derivatives into account. The spectral collocation method is used to solve the system of ODEs that follow from the transformation. This approach efficiently solves the problem by approximating the solution of the ODEs using Chebyshev polynomials of the sixth kind. Several observations are made to evaluate the approach’s effectiveness, and the convergence of the method is studied. Visual representations of the effects of different parameters on the velocity and temperature profiles provide a thorough understanding of their effects. These graphical representations offer insightful views into how the system behaves in various scenarios. The results of this investigation suggest that the mixed convection parameter and the local electric parameter both boost the velocity field. Further, the temperature field is positively impacted by the slip velocity, thermal conductivity, and Eckert numbers. These findings imply that altering these variables will have an impact on the system’s fluid flow and heat transfer properties.