Optimization over the Pareto front of nonconvex multi-objective optimal control problems
IF 1.6
2区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 3
Abstract
Abstract Simultaneous optimization of multiple objective functions results in a set of trade-off, or Pareto, solutions. Choosing a, in some sense, best solution in this set is in general a challenging task: In the case of three or more objectives the Pareto front is usually difficult to view, if not impossible, and even in the case of just two objectives constructing the whole Pareto front so as to visually inspect it might be very costly. Therefore, optimization over the Pareto (or efficient) set has been an active area of research. Although there is a wealth of literature involving finite dimensional optimization problems in this area, there is a lack of problem formulation and numerical methods for optimal control problems, except for the convex case. In this paper, we formulate the problem of optimizing over the Pareto front of nonconvex constrained and time-delayed optimal control problems as a bi-level optimization problem. Motivated by existing solution differentiability results, we propose an algorithm incorporating (i) the Chebyshev scalarization, (ii) a concept of the essential interval of weights, and (iii) the simple but effective bisection method, for optimal control problems with two objectives. We illustrate the working of the algorithm on two example problems involving an electric circuit and treatment of tuberculosis and discuss future lines of research for new computational methods.
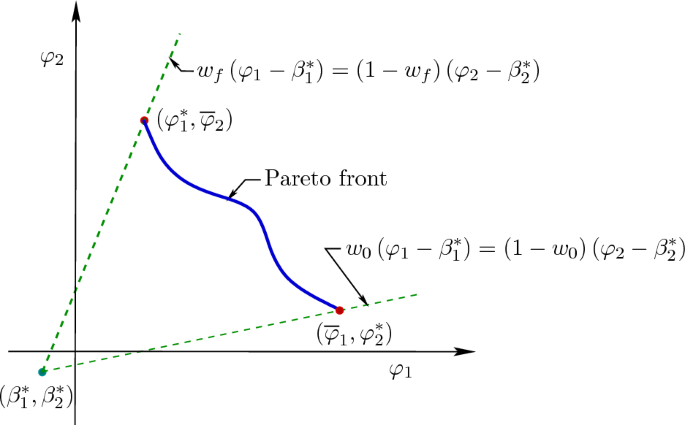
非凸多目标最优控制问题的Pareto前优化
摘要多目标函数同时优化会得到一组权衡解,即帕累托解。从某种意义上说,在这个集合中选择一个最佳解决方案通常是一项具有挑战性的任务:在有三个或更多目标的情况下,如果不是不可能的话,通常很难看到帕累托前沿,甚至在只有两个目标的情况下,构建整个帕累托前沿以直观地检查它可能会非常昂贵。因此,在帕累托(或有效)集上的优化一直是一个活跃的研究领域。尽管在这一领域有大量涉及有限维优化问题的文献,但除了凸情况外,缺乏最优控制问题的问题表述和数值方法。本文将非凸约束时滞最优控制问题的Pareto前优化问题表述为一个双级优化问题。在已有的解可微性结果的激励下,我们提出了一种包含(i) Chebyshev标量化,(ii)权值本质区间的概念,以及(iii)简单而有效的对分法的算法,用于具有两个目标的最优控制问题。我们在涉及电路和结核病治疗的两个示例问题上说明了该算法的工作,并讨论了新计算方法的未来研究方向。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.70
自引率
9.10%
发文量
91
审稿时长
10 months
期刊介绍:
Computational Optimization and Applications is a peer reviewed journal that is committed to timely publication of research and tutorial papers on the analysis and development of computational algorithms and modeling technology for optimization. Algorithms either for general classes of optimization problems or for more specific applied problems are of interest. Stochastic algorithms as well as deterministic algorithms will be considered. Papers that can provide both theoretical analysis, along with carefully designed computational experiments, are particularly welcome.
Topics of interest include, but are not limited to the following:
Large Scale Optimization,
Unconstrained Optimization,
Linear Programming,
Quadratic Programming Complementarity Problems, and Variational Inequalities,
Constrained Optimization,
Nondifferentiable Optimization,
Integer Programming,
Combinatorial Optimization,
Stochastic Optimization,
Multiobjective Optimization,
Network Optimization,
Complexity Theory,
Approximations and Error Analysis,
Parametric Programming and Sensitivity Analysis,
Parallel Computing, Distributed Computing, and Vector Processing,
Software, Benchmarks, Numerical Experimentation and Comparisons,
Modelling Languages and Systems for Optimization,
Automatic Differentiation,
Applications in Engineering, Finance, Optimal Control, Optimal Design, Operations Research,
Transportation, Economics, Communications, Manufacturing, and Management Science.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


