Numerical Analysis of MHD Nanofluid Flow Characteristics with Heat and Mass Transfer over a Vertical Cone Subjected to Thermal Radiations and Chemical Reaction
IF 1.6
4区 物理与天体物理
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
Abstract Nanoparticles have the ability to increase the impact of convective heat transfer in the boundary layer region. An investigation is made to analysis of magnetohdrodynamic nanofluid flow with heat and mass transfer over a vertical cone in porous media under the impact of thermal radiations and chemical reaction. In addition, thermal radiations, Hall current, and viscous and Joule dissipations and chemical reaction effects are considered. Considered three different nanoparticles types namely copper, silver, and titanium dioxide with water as base fluid. The governing equations are transformed by similarity transformations into a set of non-linear ordinary differential equations involving variable coefficients. Two numerically approaches are used to solve the transformed boundary layer system Finite Difference Method (FDM) and Chebyshev-Galerkin Method (CGM). As stated in the present analysis, it is appropriate to address a number of physical mechanisms, including velocity, temperature and concentration, as well as closed-form skin friction/mass transfer/heat transfer coefficients. Different comparisons are done with previously published data in order to validate the current study under specific special circumstances, and it is determined that there is a very high degree of agreement. The main results indicated that as the Prandtl number increases, the temperature profile decreases, but it grows for higher values of the thermophoresis parameter, Brownian motion, and Eckert number. Moreover, higher Brownian motion values lead to a less prominent concentration profile. Consequently, this speeds up the cooling process and enhances the surface’s durability and strength.
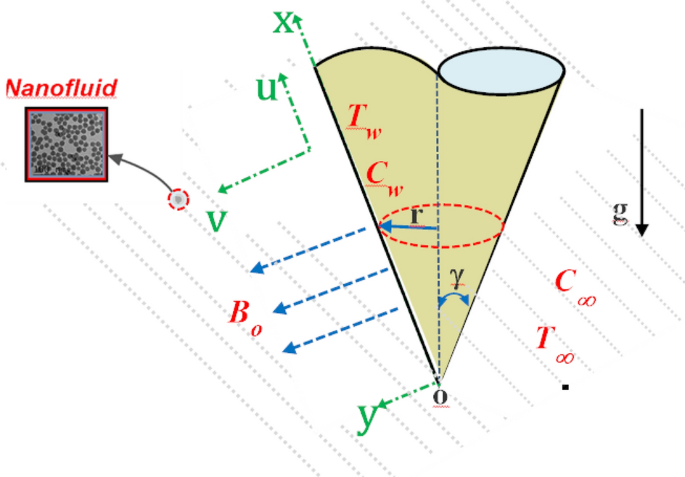
热辐射和化学反应作用下MHD纳米流体在垂直锥上传热传质特性的数值分析
摘要纳米颗粒具有增加边界层区域对流换热影响的能力。研究了在热辐射和化学反应作用下,纳米流体在多孔介质中垂直锥上的传热传质过程。此外,还考虑了热辐射、霍尔电流、粘性耗散和焦耳耗散以及化学反应效应。考虑三种不同的纳米颗粒类型,即铜、银和二氧化钛,以水为基液。通过相似变换将控制方程转化为一组非线性变系数常微分方程。采用有限差分法(FDM)和切比雪夫-伽辽金法(CGM)两种数值方法求解变换边界层系统。正如在本分析中所述,处理一些物理机制是合适的,包括速度、温度和浓度,以及封闭形式的表面摩擦/传质/传热系数。为了在特定的特殊情况下验证当前的研究,与先前发表的数据进行了不同的比较,并确定存在非常高的一致性。主要结果表明,随着普朗特数的增加,温度分布减小,但随着热泳参数、布朗运动和Eckert数的增加,温度分布增大。此外,较高的布朗运动值导致浓度曲线不太突出。因此,这加快了冷却过程,提高了表面的耐久性和强度。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Journal of Nonlinear Mathematical Physics
PHYSICS, MATHEMATICAL-PHYSICS, MATHEMATICAL
CiteScore
1.60
自引率
0.00%
发文量
67
审稿时长
3 months
期刊介绍:
Journal of Nonlinear Mathematical Physics (JNMP) publishes research papers on fundamental mathematical and computational methods in mathematical physics in the form of Letters, Articles, and Review Articles.
Journal of Nonlinear Mathematical Physics is a mathematical journal devoted to the publication of research papers concerned with the description, solution, and applications of nonlinear problems in physics and mathematics.
The main subjects are:
-Nonlinear Equations of Mathematical Physics-
Quantum Algebras and Integrability-
Discrete Integrable Systems and Discrete Geometry-
Applications of Lie Group Theory and Lie Algebras-
Non-Commutative Geometry-
Super Geometry and Super Integrable System-
Integrability and Nonintegrability, Painleve Analysis-
Inverse Scattering Method-
Geometry of Soliton Equations and Applications of Twistor Theory-
Classical and Quantum Many Body Problems-
Deformation and Geometric Quantization-
Instanton, Monopoles and Gauge Theory-
Differential Geometry and Mathematical Physics
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


