What are the optimum discrete angles to use in thermal‐infrared radiative transfer calculations?
IF 3
3区 地球科学
Q2 METEOROLOGY & ATMOSPHERIC SCIENCES
引用次数: 0
Abstract
Abstract As computer power increases, there is a need to investigate the potential gains of using more than two streams in the radiative transfer calculations of weather and climate models. In this article, seven quadrature schemes for selecting the zenith angles and weights of these streams are evaluated rigorously in terms of the accuracy of thermal‐infrared radiative transfer calculations. In addition, a new method is presented for generating “optimized” angles and weights that minimize the thermal‐infrared irradiance and heating‐rate errors for a set of clear‐sky training profiles. It is found that the standard approach of applying Gauss–Legendre quadrature in each hemisphere is the least accurate of all those tested for two and four streams. For clear‐sky irradiance calculations, “optimized” quadrature is between one and two orders of magnitude more accurate than Gauss–Legendre for any number of streams. For all‐sky calculations in which scattering becomes important, a form of Gauss–Jacobi quadrature is found to be most accurate for between four and eight streams, but with Gauss–Legendre being the most accurate for 10 or more streams. No single quadrature scheme performs best in all situations, because computing irradiances involves two different integrals over angle and the relative importance of each integral depends on the amount of scattering taking place. Additional optimized quadratures for clear‐sky and all‐sky calculations with four to eight streams are presented that constrain the relationships between angles in a way that reduces the number of exponentials that need to be computed in a radiative transfer solver.
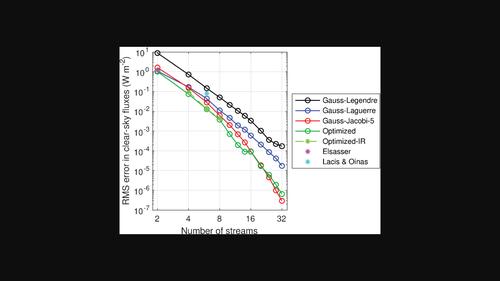
在热红外辐射传递计算中使用的最佳离散角度是什么?
随着计算机能力的提高,有必要研究在天气和气候模式的辐射传输计算中使用两种以上流的潜在收益。在本文中,根据热红外辐射传输计算的准确性,严格评估了用于选择这些流的天顶角和重量的七种正交方案。此外,提出了一种新的方法来生成“优化”的角度和权重,以最小化一组晴空训练轮廓的热红外辐照度和加热速率误差。我们发现,在两个流和四个流的所有测试中,在每个半球应用高斯-勒让德正交的标准方法是精度最低的。对于晴空辐照度计算,“优化”正交比任何数量的流高斯-勒让德更精确一到两个数量级。对于所有天空的计算,散射变得很重要,一种形式的高斯-雅可比正交被发现对4到8个流是最准确的,但高斯-勒让德对10个或更多的流是最准确的。没有单一的正交方案在所有情况下都表现最好,因为计算辐照度涉及两个不同的角度积分,每个积分的相对重要性取决于发生的散射量。提出了用于晴空和全天空计算的四到八个流的额外优化正交,以减少需要在辐射传递求解器中计算的指数数量的方式约束角度之间的关系。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
16.80
自引率
4.50%
发文量
163
审稿时长
3-8 weeks
期刊介绍:
The Quarterly Journal of the Royal Meteorological Society is a journal published by the Royal Meteorological Society. It aims to communicate and document new research in the atmospheric sciences and related fields. The journal is considered one of the leading publications in meteorology worldwide. It accepts articles, comprehensive review articles, and comments on published papers. It is published eight times a year, with additional special issues.
The Quarterly Journal has a wide readership of scientists in the atmospheric and related fields. It is indexed and abstracted in various databases, including Advanced Polymers Abstracts, Agricultural Engineering Abstracts, CAB Abstracts, CABDirect, COMPENDEX, CSA Civil Engineering Abstracts, Earthquake Engineering Abstracts, Engineered Materials Abstracts, Science Citation Index, SCOPUS, Web of Science, and more.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


