Constructions of homotopy 4-spheres by pochette surgery
IF 0.5
4区 数学
Q3 MATHEMATICS
引用次数: 1
Abstract
Abstract The boundary sum of the product of a circle with a 3-ball and the product of a disk with a 2-sphere is called a pochette. Pochette surgery, which was discovered by Iwase and Matsumoto, is a generalization of Gluck surgery and a special case of torus surgery. For a pochette P embedded in a 4-manifold X , a pochette surgery on X is the operation of removing the interior of P and gluing P by a diffeomorphism of the boundary of P . We present an explicit diffeomorphism of the boundary of P for constructing a 4-manifold after any pochette surgery. We also describe a necessary and sufficient condition for some pochette surgeries on any simply-connected closed 4-manifold create a 4-manifold with the same homotopy type of the original 4-manifold. In this paper we construct infinitely many embeddings of a pochette into the 4-sphere and prove that homotopy 4-spheres obtained from surgeries along these embedded pochettes are all diffeomorphic to the 4-sphere by some explicit handle calculus and relative handle calculus.
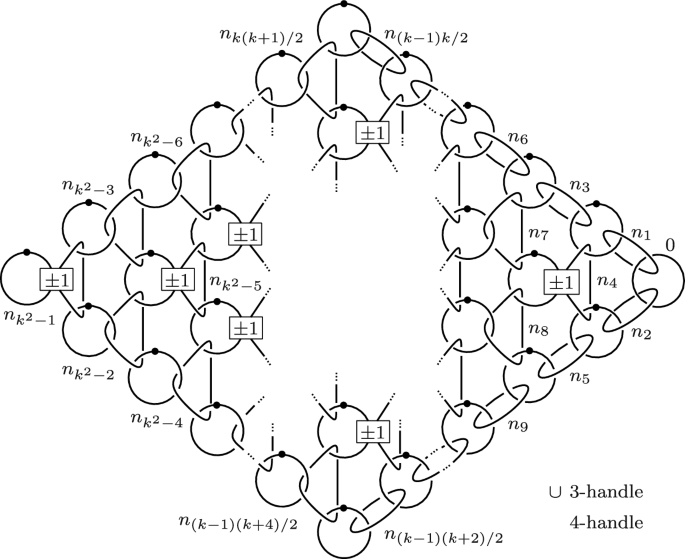
用pochette手术构造同伦4球
圆与三球之积的边界和与圆盘与二球之积的边界和称为波切特。Pochette手术是由Iwase和Matsumoto发现的,它是Gluck手术的推广,是环体手术的一个特例。对于嵌入在4流形X中的凹形P,对X的凹形手术是去除P的内部并通过P边界的微分同构粘接P的操作。我们给出了任意波切手术后构造一个4流形的P边界的显微分同构。我们还描述了在任意单连通闭合4流形上的一些pochette手术能产生与原4流形相同同伦类型的4流形的充分必要条件。本文在4球上构造了无限多个凹凹点,并利用显式柄微积分和相对柄微积分证明了沿这些凹凹点进行手术得到的同伦4球与4球都是微分同构的。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Geometriae Dedicata
数学-数学
CiteScore
0.90
自引率
0.00%
发文量
78
审稿时长
4-8 weeks
期刊介绍:
Geometriae Dedicata concentrates on geometry and its relationship to topology, group theory and the theory of dynamical systems.
Geometriae Dedicata aims to be a vehicle for excellent publications in geometry and related areas. Features of the journal will include:
A fast turn-around time for articles.
Special issues centered on specific topics.
All submitted papers should include some explanation of the context of the main results.
Geometriae Dedicata was founded in 1972 on the initiative of Hans Freudenthal in Utrecht, the Netherlands, who viewed geometry as a method rather than as a field. The present Board of Editors tries to continue in this spirit. The steady growth of the journal since its foundation is witness to the validity of the founder''s vision and to the success of the Editors'' mission.
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


