Enhancing cluster analysis via topological manifold learning

Abstract

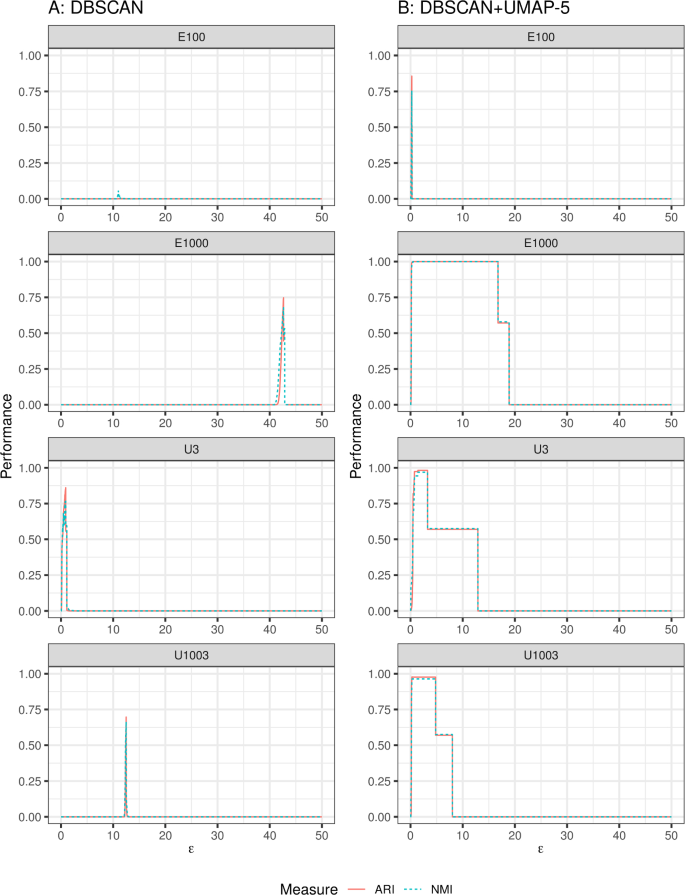
Abstract We discuss topological aspects of cluster analysis and show that inferring the topological structure of a dataset before clustering it can considerably enhance cluster detection: we show that clustering embedding vectors representing the inherent structure of a dataset instead of the observed feature vectors themselves is highly beneficial. To demonstrate, we combine manifold learning method UMAP for inferring the topological structure with density-based clustering method DBSCAN. Synthetic and real data results show that this both simplifies and improves clustering in a diverse set of low- and high-dimensional problems including clusters of varying density and/or entangled shapes. Our approach simplifies clustering because topological pre-processing consistently reduces parameter sensitivity of DBSCAN. Clustering the resulting embeddings with DBSCAN can then even outperform complex methods such as SPECTACL and ClusterGAN. Finally, our investigation suggests that the crucial issue in clustering does not appear to be the nominal dimension of the data or how many irrelevant features it contains, but rather how separable the clusters are in the ambient observation space they are embedded in, which is usually the (high-dimensional) Euclidean space defined by the features of the data. The approach is successful because it performs the cluster analysis after projecting the data into a more suitable space that is optimized for separability, in some sense.