Optimal investment and consumption for financial markets with jumps under transaction costs

Abstract

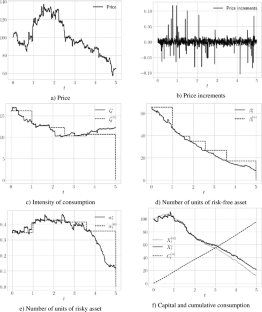
We consider a portfolio optimisation problem for financial markets described by semimartingales with independent increments and jumps defined through Lévy processes. First, for power utility functions, we show a corresponding verification theorem and then find optimal consumption/investment strategies in an explicit form. Moreover, on the basis of the strategies constructed using the Leland–Lépinette approach, we develop an asymptotic optimal investment and consumption method for financial markets with proportional transaction costs when the number of portfolio revisions tends to infinity. Finally, we provide Monte Carlo simulations to numerically illustrate the obtained results in practice.