Optimal Protocols for Quantum Metrology with Noisy Measurements
IF 11
Q1 PHYSICS, APPLIED
引用次数: 4
Abstract
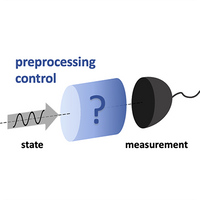
Measurement noise is a major source of noise in quantum metrology. Here, we explore preprocessing protocols that apply quantum controls to the quantum sensor state prior to the final noisy measurement (but after the unknown parameter has been imparted), aiming to maximize the estimation precision. We define the quantum preprocessing-optimized Fisher information, which determines the ultimate precision limit for quantum sensors under measurement noise, and conduct a thorough investigation into optimal preprocessing protocols. First, we formulate the preprocessing optimization problem as a biconvex optimization using the error observable formalism, based on which we prove that unitary controls are optimal for pure states and derive analytical solutions of the optimal controls in several practically relevant cases. Then we prove that for classically mixed states (whose eigenvalues encode the unknown parameter) under commuting-operator measurements, coarse-graining controls are optimal, while unitary controls are suboptimal in certain cases. Finally, we demonstrate that in multiprobe systems where noisy measurements act independently on each probe, the noiseless precision limit can be asymptotically recovered using global controls for a wide range of quantum states and measurements. Applications to noisy Ramsey interferometry and thermometry are presented, as well as explicit circuit constructions of optimal controls.Received 20 March 2023Revised 9 August 2023Accepted 8 September 2023DOI:https://doi.org/10.1103/PRXQuantum.4.040305Published by the American Physical Society under the terms of the Creative Commons Attribution 4.0 International license. Further distribution of this work must maintain attribution to the author(s) and the published article's title, journal citation, and DOI.Published by the American Physical SocietyPhysics Subject Headings (PhySH)Research AreasQuantum Fisher informationQuantum fluctuations & noiseQuantum information theoryQuantum metrologyQuantum sensingQuantum Information, Science & Technology
带噪声测量的量子计量的最佳方案
测量噪声是量子测量中的主要噪声源。在这里,我们探索了在最终噪声测量之前(但在未知参数被赋予之后)对量子传感器状态应用量子控制的预处理协议,旨在最大化估计精度。我们定义了量子预处理优化的Fisher信息,它决定了量子传感器在测量噪声下的最终精度极限,并对最佳预处理协议进行了深入的研究。首先,我们利用误差可观察的形式将预处理优化问题表述为一个双凸优化问题,在此基础上,我们证明了单一控制对于纯状态是最优的,并在几个实际相关案例中推导了最优控制的解析解。然后我们证明了在交换算子测量下,对于典型混合状态(其特征值编码未知参数),粗粒度控制在某些情况下是最优的,而单一控制在某些情况下是次优的。最后,我们证明了在噪声测量独立作用于每个探针的多探针系统中,使用广泛的量子态和测量的全局控制可以渐近恢复无噪声精度极限。介绍了在噪声拉姆齐干涉测量和温度测量中的应用,以及最优控制的显式电路结构。根据知识共享署名4.0国际许可协议,美国物理学会于2023年9月8日接受doi:https://doi.org/10.1103/PRXQuantum.4.040305Published。这项工作的进一步分发必须保持作者的归属和已发表文章的标题,期刊引用和DOI。发表于美国物理学会物理学科标题(PhySH)研究领域量子费雪信息量子涨落与噪声量子信息论量子计量量子传感量子信息科学与技术
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


