The difference between port-Hamiltonian, passive and positive real descriptor systems

IF 1.8 4区计算机科学 Q3 AUTOMATION & CONTROL SYSTEMS

Mathematics of Control Signals and Systems Pub Date : 2023-11-11 DOI:10.1007/s00498-023-00373-2

Karim Cherifi, Hannes Gernandt, Dorothea Hinsen

引用次数: 6

Abstract

Abstract The relation between passive and positive real systems has been extensively studied in the literature. In this paper, we study their connection to the more recently used notion of port-Hamiltonian descriptor systems. It is well-known that port-Hamiltonian systems are passive and that passive systems are positive real. Hence it is studied under which assumptions the converse implications hold. Furthermore, the relationship between passivity and KYP inequalities is investigated.

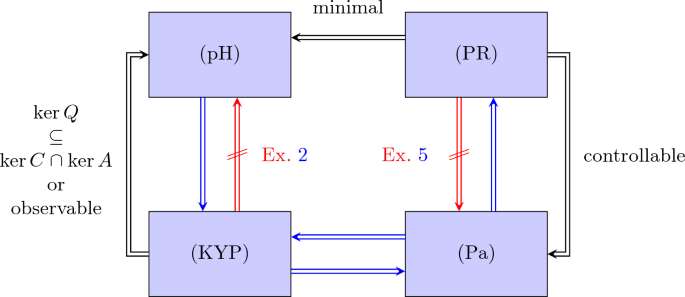
Abstract Image

查看原文本刊更多论文

波特-哈密顿系统、被动实描述子系统和正实描述子系统的区别

被动实系统和积极实系统之间的关系在文献中得到了广泛的研究。在本文中，我们研究了它们与最近使用的端口-哈密顿描述系统概念的联系。众所周知，波特-哈密顿系统是被动的，而被动系统是正实的。因此，研究在哪些假设下，相反的含义成立。进一步研究了被动性与KYP不等式之间的关系。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Mathematics of Control Signals and Systems 工程技术-工程：电子与电气

CiteScore

2.90

自引率

0.00%

发文量

审稿时长

>12 weeks

期刊介绍： Mathematics of Control, Signals, and Systems (MCSS) is an international journal devoted to mathematical control and system theory, including system theoretic aspects of signal processing. Its unique feature is its focus on mathematical system theory; it concentrates on the mathematical theory of systems with inputs and/or outputs and dynamics that are typically described by deterministic or stochastic ordinary or partial differential equations, differential algebraic equations or difference equations. Potential topics include, but are not limited to controllability, observability, and realization theory, stability theory of nonlinear systems, system identification, mathematical aspects of switched, hybrid, networked, and stochastic systems, and system theoretic aspects of optimal control and other controller design techniques. Application oriented papers are welcome if they contain a significant theoretical contribution.