Reliability analysis and uncertainty quantification of clay and sand slopes stability evaluated by Fellenius and Bishop’s simplified methods
IF 7.1
Q2 ENGINEERING, GEOLOGICAL
引用次数: 0
Abstract
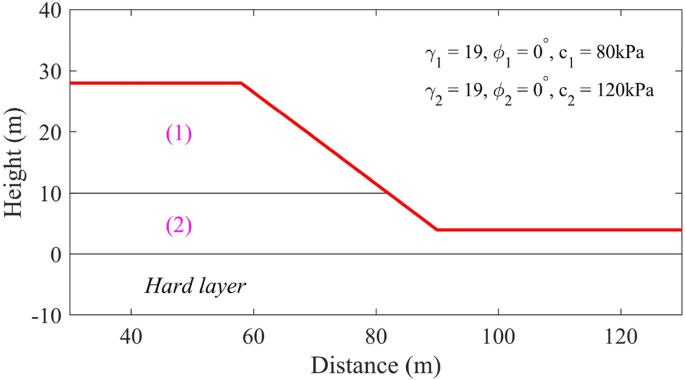
Abstract Slope stabilities are mainly designed using the conventional design approach (CDA), where the limit equilibrium methods (LEMs) are performed. Fellenius and Bishop’s simplified methods are the two commonly LEMs adopted as recommended in most design codes. In the design process of CDA, the safety factors (FS) of slopes are checked with specified FSs to ensure stability. The CDA has inherent drawbacks because the design process does not account for uncertainties. Moreover, different LEMs using different assumptions to solve the safety factors might include some amount orders of approximations. This study conducts probabilistic analyses, i.e., Monte Carlo simulations (MCSs) and uncertainty quantification, to obtain insights into the two LEMs applied to clay and sand slopes. The results reveal that the reliability indexes (RIs) obtained from the two LEMs-based MCSs are relatively identical for the same slope. Concerning the soil types, however, the RIs of the clay slope are significantly lower than those estimated for the sand slope, regardless of the LEMs used. The uncertainty quantifications for the clay slopes reveal that the two LEMs have relatively similar bias factors regarding FSs. Nevertheless, using the Fellenius method underestimates the probabilistic safety (about 17% in terms of the mean of FSs) for the sand slope compared to Bishop’s simplified method. Moreover, the coefficients of variation of FS obtained from the clay slope are consistently larger than those from the sand slope. These observations imply that the clay slope is more uncertain than the sand slope, and the Fellenius method results in lower FSs for sand slopes. Therefore, the FSs specified in the design codes should be connected to the soil type or the LEMs used to achieve the same probabilistic safety levels. Finally, the equivalent FSs associated with a RI of 1.75 are derived for each slope and each LEM used.
用felenius和Bishop的简化方法评价粘土和砂土边坡稳定性的可靠度分析和不确定度量化
摘要边坡稳定性设计主要采用常规设计方法(CDA),其中采用极限平衡法(lem)进行设计。费勒纽斯法和毕晓普法是大多数设计规范中推荐采用的两种最常用的lem。在CDA的设计过程中,采用规定的安全系数对边坡进行校核,以保证边坡的稳定性。由于设计过程不考虑不确定性,CDA具有固有的缺点。此外,使用不同假设来求解安全系数的不同lem可能包含一些数量阶的近似。本研究通过概率分析,即蒙特卡罗模拟(mcs)和不确定性量化,来深入了解这两种lem在粘土和砂土边坡中的应用。结果表明,对于相同的坡度,两种基于lems的MCSs得到的可靠度指标(RIs)相对相同。然而,就土壤类型而言,无论使用何种lem,粘土边坡的RIs都明显低于砂质边坡的RIs。对粘土边坡的不确定度量化表明,两种lem在FSs方面具有相对相似的偏差因子。然而,与Bishop的简化方法相比,使用Fellenius方法低估了砂坡的概率安全性(以FSs平均值计算约为17%)。此外,粘土边坡的FS变异系数始终大于砂坡。这些观测结果表明,粘土边坡比砂边坡具有更大的不确定性,并且费伦尤斯方法对砂边坡的FSs较低。因此,设计规范中规定的FSs应与土壤类型或lem相连接,以达到相同的概率安全水平。最后,推导出每个坡度和每个LEM的等效FSs,其RI值为1.75。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

International Journal of Geo-Engineering
ENGINEERING, GEOLOGICAL-
CiteScore
3.70
自引率
0.00%
发文量
10
审稿时长
13 weeks
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


