Bayesian joint quantile autoregression

Abstract

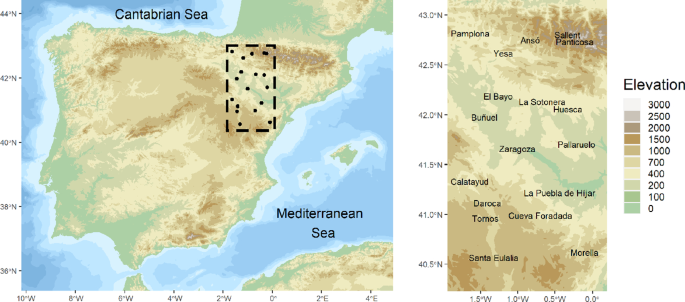
Abstract Quantile regression continues to increase in usage, providing a useful alternative to customary mean regression. Primary implementation takes the form of so-called multiple quantile regression, creating a separate regression for each quantile of interest. However, recently, advances have been made in joint quantile regression, supplying a quantile function which avoids crossing of the regression across quantiles. Here, we turn to quantile autoregression (QAR), offering a fully Bayesian version. We extend the initial quantile regression work of Koenker and Xiao (J Am Stat Assoc 101(475):980–990, 2006. https://doi.org/10.1198/016214506000000672 ) in the spirit of Tokdar and Kadane (Bayesian Anal 7(1):51–72, 2012. https://doi.org/10.1214/12-BA702 ). We offer a directly interpretable parametric model specification for QAR. Further, we offer a pth-order QAR(p) version, a multivariate QAR(1) version, and a spatial QAR(1) version. We illustrate with simulation as well as a temperature dataset collected in Aragón, Spain.