A nested genetic algorithm strategy for an optimal seismic design of frames
IF 1.6
2区 数学
Q2 MATHEMATICS, APPLIED
引用次数: 0
Abstract
Abstract An innovative strategy for an optimal design of planar frames able to resist seismic excitations is proposed. The optimal design is performed considering the cross sections of beams and columns as design variables. The procedure is based on genetic algorithms (GA) that are performed according to a nested structure suitable to be implemented in parallel on several computing devices. In particular, this bi-level optimization involves two nested genetic algorithms. The first external one seeks the size of the structural elements of the frame which corresponds to the most performing solution associated with the highest value of an appropriate fitness function. The latter function takes into account, among other considerations, the seismic safety factor and the failure mode that are calculated by means of the second internal algorithm. The proposed procedure aims at representing a prompt performance-based design procedure which observes earthquake engineering principles, that is displacement capacity and energy dissipation, although based on a limit analysis, thus avoiding the need of performing cumbersome nonlinear analyses. The details of the proposed procedure are provided and applications to the seismic design of two frames of different size are described.
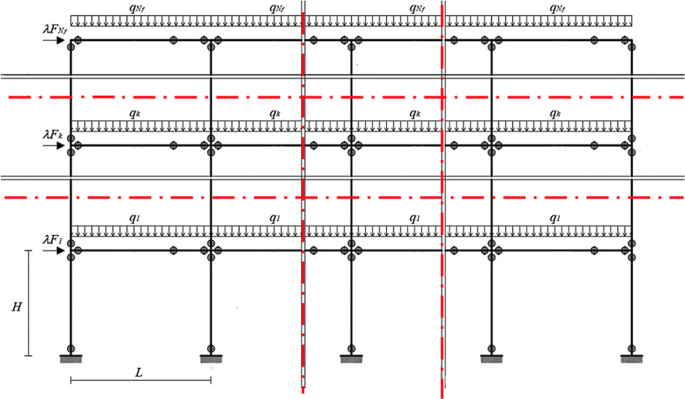
框架抗震优化设计的嵌套遗传算法策略
摘要提出了一种抗地震作用平面框架优化设计的创新策略。以梁、柱截面为设计变量进行优化设计。该过程基于遗传算法(GA),该算法根据适合在多个计算设备上并行实现的嵌套结构执行。特别地,这种双层优化涉及两个嵌套的遗传算法。第一个外部函数寻求框架结构元素的大小,它对应于与适当适应度函数的最高值相关联的最有效的解决方案。后一函数除考虑其他因素外,还考虑了地震安全系数和破坏模式,这些是通过第二种内部算法计算出来的。所提出的程序旨在表示一种快速的基于性能的设计程序,该程序遵循地震工程原则,即位移能力和能量耗散,尽管基于极限分析,从而避免了执行繁琐的非线性分析的需要。文中还详细介绍了该方法在两种不同尺寸框架抗震设计中的应用。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊
CiteScore
3.70
自引率
9.10%
发文量
91
审稿时长
10 months
期刊介绍:
Computational Optimization and Applications is a peer reviewed journal that is committed to timely publication of research and tutorial papers on the analysis and development of computational algorithms and modeling technology for optimization. Algorithms either for general classes of optimization problems or for more specific applied problems are of interest. Stochastic algorithms as well as deterministic algorithms will be considered. Papers that can provide both theoretical analysis, along with carefully designed computational experiments, are particularly welcome.
Topics of interest include, but are not limited to the following:
Large Scale Optimization,
Unconstrained Optimization,
Linear Programming,
Quadratic Programming Complementarity Problems, and Variational Inequalities,
Constrained Optimization,
Nondifferentiable Optimization,
Integer Programming,
Combinatorial Optimization,
Stochastic Optimization,
Multiobjective Optimization,
Network Optimization,
Complexity Theory,
Approximations and Error Analysis,
Parametric Programming and Sensitivity Analysis,
Parallel Computing, Distributed Computing, and Vector Processing,
Software, Benchmarks, Numerical Experimentation and Comparisons,
Modelling Languages and Systems for Optimization,
Automatic Differentiation,
Applications in Engineering, Finance, Optimal Control, Optimal Design, Operations Research,
Transportation, Economics, Communications, Manufacturing, and Management Science.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


