Non-reductive geometric invariant theory and hyperbolicity
IF 3.6
1区 数学
Q1 MATHEMATICS
引用次数: 11
Abstract
Abstract The Green–Griffiths–Lang and Kobayashi hyperbolicity conjectures for generic hypersurfaces of polynomial degree are proved using intersection theory for non-reductive geometric invariant theoretic quotients and recent work of Riedl and Yang.
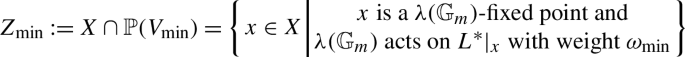
非约化几何不变理论与双曲性
利用非约化几何不变理论商的交理论和Riedl和Yang的最新工作证明了多项式次一般超曲面的Green-Griffiths-Lang和Kobayashi双曲猜想。
本文章由计算机程序翻译,如有差异,请以英文原文为准。
求助全文
约1分钟内获得全文
求助全文
来源期刊

Inventiones mathematicae
数学-数学
CiteScore
5.60
自引率
3.20%
发文量
76
审稿时长
12 months
期刊介绍:
This journal is published at frequent intervals to bring out new contributions to mathematics. It is a policy of the journal to publish papers within four months of acceptance. Once a paper is accepted it goes immediately into production and no changes can be made by the author(s).
 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


