A Remark on the Uniqueness of Solutions to Hyperbolic Conservation Laws

Abstract

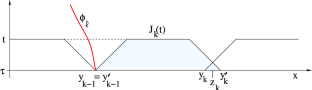
Given a strictly hyperbolic \(n\times n\) system of conservation laws, it is well known that there exists a unique Lipschitz semigroup of weak solutions, defined on a domain of functions with small total variation, which are limits of vanishing viscosity approximations. The aim of this note is to prove that every weak solution taking values in the domain of the semigroup, and whose shocks satisfy the Liu admissibility conditions, actually coincides with a semigroup trajectory.