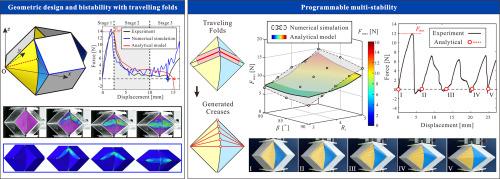
Programmable multi-stability of curved-crease origami structures with travelling folds

Multi-stable structures capable of rapid switching among different stable states have seen applications in various fields such as energy absorption, mechanical computing, and soft actuators. Curved-crease origami, which naturally involves simultaneous deformation of creases and facets, shows great potential in the development of multi-stable structures. However, upon loading, existing curved-crease origami structures tend to follow the same deformation mode as in the curved surface formation process which involves facets elastic bending, flattening, and reverse bending, thus leading to only two stable states. To achieve multi-stability, here we propose a series of curved-crease origami structures composed of planar facets and curved ones. Through a combination of experiments, numerical simulations, and analytical modelling, we demonstrate that the planar facets forming a Sarrus linkage guide the deformation mode of the curved ones, leading to the initiation and propagation of travelling folds in the curved facets. By transforming the travelling folds at specific positions into actual creases, we can achieve multiple stable states in a single structure. In addition, the number and positions of the stable states, as well as the initial peak force, can be programmed by varying the geometric parameters. Consequently, this work opens a new pathway for the development of generic multi-stable structures with programmable mechanical properties.