瞬态动力学神经物理模拟器非滚动训练中的可分性
IF 6.9
1区 工程技术
Q1 ENGINEERING, MULTIDISCIPLINARY
Computer Methods in Applied Mechanics and Engineering
Pub Date : 2024-10-23
DOI:10.1016/j.cma.2024.117441
引用次数: 0
摘要
随着时间推移展开训练轨迹会严重影响神经网络增强物理模拟器的推理精度。我们通过研究在离散地面实况轨迹上训练神经网络的三种变体来分析这些影响。除了常用的单步设置和完全可微分展开外,我们还采用了第三种应用较少的变体:无时间梯度展开。通过比较使用这三种模式训练的网络,我们可以区分开卷的两种主要影响:训练分布偏移和长期梯度。我们对各种物理系统、网络规模、网络架构、训练设置和测试场景进行了详细研究。研究还包括计算模拟轨迹的两种模式。在预测设置中,我们完全依靠神经网络来计算轨迹。相比之下,修正设置包括一个由神经网络支持的数值求解器。我们的研究跨越了所有这些变化,为我们的主要发现提供了经验基础:与不使用数值求解器的完全可微分预测设置相比,在修正设置中使用数值求解器支持的非可微分但未滚动的训练设置,可以产生实质性的改进。我们还量化了在完全可微分设置下训练的模型与非可微分模型在准确性上的差异。在直接比较校正网络时,可微分设置表现最佳,而在相互比较预测设置时也是如此。在这两种情况下,无时间梯度展开的准确性都比较接近。此外,我们通过经验证明,这些行为不受底层物理系统、网络结构和大小以及数值方案变化的影响。这些结果促使我们在无法获得完全可微分性的情况下,也能将无微分数值模拟器集成到训练设置中。我们还发现,与数值算法相比,普通神经架构的收敛速度较低。这就鼓励使用结合神经算法和数值算法的修正方法,以利用两者的优势。本文章由计算机程序翻译,如有差异,请以英文原文为准。
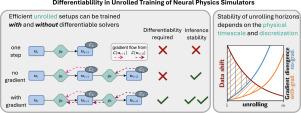
Differentiability in unrolled training of neural physics simulators on transient dynamics
Unrolling training trajectories over time strongly influences the inference accuracy of neural network-augmented physics simulators. We analyze these effects by studying three variants of training neural networks on discrete ground truth trajectories. In addition to commonly used one-step setups and fully differentiable unrolling, we include a third, less widely used variant: unrolling without temporal gradients. Comparing networks trained with these three modalities makes it possible to disentangle the two dominant effects of unrolling, training distribution shift and long-term gradients. We present a detailed study across physical systems, network sizes, network architectures, training setups, and test scenarios. It also encompasses two modes of computing the simulation trajectories. In prediction setups, we rely solely on neural networks to compute a trajectory. In contrast, correction setups include a numerical solver that is supported by a neural network. Spanning all these variations, our study provides the empirical basis for our main findings: A non-differentiable but unrolled training setup supported by a numerical solver in a correction setup can yield substantial improvements over a fully differentiable prediction setup not utilizing this solver. We also quantify a difference in the accuracy of models trained in a fully differentiable setup compared to their non-differentiable counterparts. Differentiable setups perform best in a direct comparison of correction networks, and the same is observed when comparing prediction setups among each other. In both cases, the accuracy of unrolling without temporal gradients comes relatively close. Furthermore, we empirically show that these behaviors are invariant to changes in the underlying physical system, the network architecture and size, and the numerical scheme. These results motivate integrating non-differentiable numerical simulators into training setups even if full differentiability is unavailable. We also observe that the convergence rate of common neural architectures is low compared to numerical algorithms. This encourages the use of correction approaches combining neural and numerical algorithms to utilize the benefits of both.
求助全文
通过发布文献求助,成功后即可免费获取论文全文。
去求助
来源期刊
CiteScore
12.70
自引率
15.30%
发文量
719
审稿时长
44 days
期刊介绍:
Computer Methods in Applied Mechanics and Engineering stands as a cornerstone in the realm of computational science and engineering. With a history spanning over five decades, the journal has been a key platform for disseminating papers on advanced mathematical modeling and numerical solutions. Interdisciplinary in nature, these contributions encompass mechanics, mathematics, computer science, and various scientific disciplines. The journal welcomes a broad range of computational methods addressing the simulation, analysis, and design of complex physical problems, making it a vital resource for researchers in the field.

 求助内容:
求助内容: 应助结果提醒方式:
应助结果提醒方式:


