The energy of 180° domain walls of uniaxial crystals with the different magnetocrystalline anisotropy type

IF 2.5 3区材料科学 Q3 MATERIALS SCIENCE, MULTIDISCIPLINARY

Journal of Magnetism and Magnetic Materials Pub Date : 2024-09-29 DOI:10.1016/j.jmmm.2024.172560

A.I. Sinkevich, M.B. Lyakhova, E.M. Semenova

{"title":"The energy of 180° domain walls of uniaxial crystals with the different magnetocrystalline anisotropy type","authors":"A.I. Sinkevich, M.B. Lyakhova, E.M. Semenova","doi":"10.1016/j.jmmm.2024.172560","DOIUrl":null,"url":null,"abstract":"<div><div>The main aim of the present work is to analyze the magnetocrystalline anisotropy (MCA) energy function of uniaxial crystals and to derive analytical expressions for the domain wall (DW) energy taking into account two MCA constants. Thus, the article presents a detailed analysis of the magnetocrystalline anisotropy energy function of uniaxial crystals taking into account two MCA constants (K1, K2). The values of the MCA energy extremes and the position of the easy magnetization directions (EMD) and hard magnetization directions (HMD) were determined. The MCA diagram was plotted in “K1”-“K2” coordinates. Six types of MCA have been found for uniaxial crystals. Two of them are simple with one maximum and one minimum of the EA(θ) function, and four are complex with two absolute and one local extreme for each. It is shown that EA(K1, K2) function has the smallest difference between the maximum and minimum values equal to |K1|/4 and the smallest angle between EMD and HMD equal to π/4 when the K1 + K2 = 0 condition is met. Analytical expressions for the 180° Bloch domain wall energy surface density (γ) were derived for uniaxial crystals with each MCA type. It is found that the γ(K1, K2) function has a minimum, equal to <math><mrow><mi>γ</mi><mo>=</mo><mn>2</mn><msqrt><mrow><mrow><mi>A</mi><mo>|</mo></mrow><msub><mi>K</mi><mn>1</mn></msub><mrow><mo>|</mo></mrow></mrow></msqrt></mrow></math> when the relation K1 + K2 = 0 between MCA constants is satisfied. The derived analytical expressions are useful for a detailed spin-reorientation transition analysis. To illustrate this, examples of the application of the obtained results to MCA analyses of real crystals and DW energy calculations are given.</div></div>","PeriodicalId":366,"journal":{"name":"Journal of Magnetism and Magnetic Materials","volume":"610 ","pages":"Article 172560"},"PeriodicalIF":2.5000,"publicationDate":"2024-09-29","publicationTypes":"Journal Article","fieldsOfStudy":null,"isOpenAccess":false,"openAccessPdf":"","citationCount":"0","resultStr":null,"platform":"Semanticscholar","paperid":null,"PeriodicalName":"Journal of Magnetism and Magnetic Materials","FirstCategoryId":"88","ListUrlMain":"https://www.sciencedirect.com/science/article/pii/S0304885324008515","RegionNum":3,"RegionCategory":"材料科学","ArticlePicture":[],"TitleCN":null,"AbstractTextCN":null,"PMCID":null,"EPubDate":"","PubModel":"","JCR":"Q3","JCRName":"MATERIALS SCIENCE, MULTIDISCIPLINARY","Score":null,"Total":0}

引用次数: 0

Abstract

The main aim of the present work is to analyze the magnetocrystalline anisotropy (MCA) energy function of uniaxial crystals and to derive analytical expressions for the domain wall (DW) energy taking into account two MCA constants. Thus, the article presents a detailed analysis of the magnetocrystalline anisotropy energy function of uniaxial crystals taking into account two MCA constants (K₁, K₂). The values of the MCA energy extremes and the position of the easy magnetization directions (EMD) and hard magnetization directions (HMD) were determined. The MCA diagram was plotted in “K₁”-“K₂” coordinates. Six types of MCA have been found for uniaxial crystals. Two of them are simple with one maximum and one minimum of the E_A(θ) function, and four are complex with two absolute and one local extreme for each. It is shown that E_A(K₁, K₂) function has the smallest difference between the maximum and minimum values equal to |K₁|/4 and the smallest angle between EMD and HMD equal to π/4 when the K₁ + K₂ = 0 condition is met. Analytical expressions for the 180° Bloch domain wall energy surface density (γ) were derived for uniaxial crystals with each MCA type. It is found that the γ(K₁, K₂) function has a minimum, equal to

γ = 2 \sqrt{A | K_{1} |}

when the relation K₁ + K₂ = 0 between MCA constants is satisfied. The derived analytical expressions are useful for a detailed spin-reorientation transition analysis. To illustrate this, examples of the application of the obtained results to MCA analyses of real crystals and DW energy calculations are given.

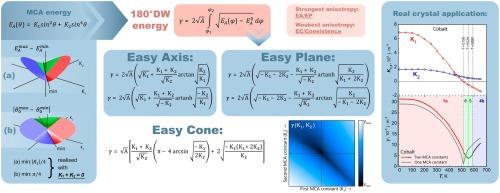
Abstract Image

查看原文本刊更多论文

不同磁晶各向异性类型单轴晶体 180° 域壁的能量

本研究的主要目的是分析单轴晶体的磁晶各向异性（MCA）能量函数，并在考虑两个 MCA 常量的情况下推导出畴壁（DW）能量的分析表达式。因此，文章详细分析了考虑两个 MCA 常量（K1、K2）的单轴晶体磁晶各向异性能量函数。确定了 MCA 能量极值以及易磁化方向（EMD）和硬磁化方向（HMD）的位置。MCA 图以 "K1"-"K2 "坐标绘制。在单轴晶体中发现了六种类型的 MCA。其中两种是简单的，EA(θ) 函数只有一个最大值和一个最小值；四种是复杂的，各有两个绝对极值和一个局部极值。结果表明，当 K1 + K2 = 0 条件满足时，EA(K1, K2) 函数的最大值和最小值之差最小，等于 |K1|/4，EMD 和 HMD 之间的夹角最小，等于 π/4。针对每种 MCA 类型的单轴晶体，推导出了 180° 布洛赫畴壁能量表面密度 (γ)的分析表达式。结果发现，当 MCA 常量之间的关系 K1 + K2 = 0 满足时，γ(K1, K2) 函数有一个最小值，等于 γ=2A|K1|。推导出的分析表达式有助于进行详细的自旋取向转变分析。为了说明这一点，我们举例说明了所获结果在实际晶体的 MCA 分析和 DW 能量计算中的应用。

本文章由计算机程序翻译，如有差异，请以英文原文为准。

求助全文

约1分钟内获得全文求助全文

来源期刊

Journal of Magnetism and Magnetic Materials 物理-材料科学：综合

CiteScore

5.30

自引率

11.10%

发文量

1149

审稿时长

59 days

期刊介绍： The Journal of Magnetism and Magnetic Materials provides an important forum for the disclosure and discussion of original contributions covering the whole spectrum of topics, from basic magnetism to the technology and applications of magnetic materials. The journal encourages greater interaction between the basic and applied sub-disciplines of magnetism with comprehensive review articles, in addition to full-length contributions. In addition, other categories of contributions are welcome, including Critical Focused issues, Current Perspectives and Outreach to the General Public. Main Categories: Full-length articles: Technically original research documents that report results of value to the communities that comprise the journal audience. The link between chemical, structural and microstructural properties on the one hand and magnetic properties on the other hand are encouraged. In addition to general topics covering all areas of magnetism and magnetic materials, the full-length articles also include three sub-sections, focusing on Nanomagnetism, Spintronics and Applications. The sub-section on Nanomagnetism contains articles on magnetic nanoparticles, nanowires, thin films, 2D materials and other nanoscale magnetic materials and their applications. The sub-section on Spintronics contains articles on magnetoresistance, magnetoimpedance, magneto-optical phenomena, Micro-Electro-Mechanical Systems (MEMS), and other topics related to spin current control and magneto-transport phenomena. The sub-section on Applications display papers that focus on applications of magnetic materials. The applications need to show a connection to magnetism. Review articles: Review articles organize, clarify, and summarize existing major works in the areas covered by the Journal and provide comprehensive citations to the full spectrum of relevant literature.